Verhältnis von Mengen
In der Mengenlehre können wir die Mengen nicht nur auf ihre Mächtigkeit und Gleichheit prüfen, sondern wir können auch das Verhältnis zweier Mengen zu einander beschreiben. Es gibt einige Verhältnisse, die sich unterscheiden. Diese wollen wir euch nun zeigen und erklären.
Teilmenge
Unter einer Teilmenge versteht man, dass eine Menge, ganz zu einer anderen Menge gehört und somit Teil der größeren Menge ist. Wir zeigen euch ein Beispiel. Die Menge B gehört zur Menge A und ist daher Teilmenge. Jedes Element aus Menge B gehört auch zur Menge A.
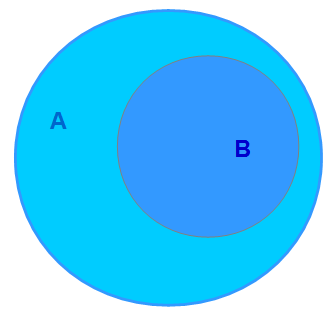
Schnittmenge
Eine Schnittmenge finden wir immer dann, wenn es Elemente in zwei Mengen gibt, die sowohl zur einen als auch zur anderen Menge gehören. Der Unterschied zur Teilmenge ist, dass beide Mengen noch Elemente beinhalten, die nicht in der anderen vorhanden sind.
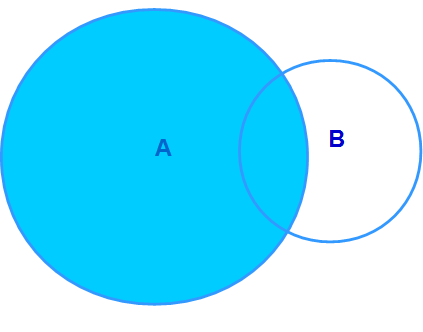
Die Abbildung zeigt eine Schnittmenge der Mengen A und B.
Unser Lernvideo zu : Verhältnis von Mengen
Differenzmenge
Unter einer Differenzmenge versteht man den Untschied der beiden Mengen. In der Differenzmenge sind alle Mengen, die nicht zur anderen Menge oder zur Schnittmenge gehört.
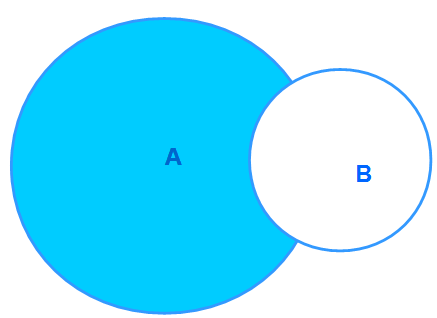
In der dargestellten Differenzmenge gehört die hellblaue Menge zwar zu A, aber nicht zur Menge B. Alle Elemente der hellblauen Fläche sind die Differenzmenge.
Komplement
Unter dem Komplement verstehen wir alle Elemente, die nicht zu einer angegebenen Menge gehören. Alle Element außerhalb der Menge B sind das Komplement zur Menge B.

