Berechnung unbekannter Winkel
Neben unbekannten Seiten kann man mit Hilfe der Trigonometrie auch unbekannte Winkel berechnen. Hierfür benötigen wir neben den normalen Sinus, Kosinus und Tangens-Funktionen noch deren Umkehrfunktionen. Die Umkehrfunktionen heißen Arkussinus, Arkuskosinus und Arkustangens. Mithilfe dieser drei Funktionen können wir die Winkel in einem Dreieck berechnen.
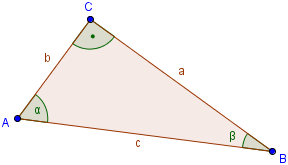
Wir kennen bereits diese Formeln:
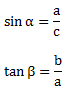
Wenn wir nun die Seiten gegeben haben und mit diesen Formeln die Winkel berechnen wollen, müssen wir sie zu dem Winkel umformen. Das können wir mithilfe der Umkehrfunktionen.
Lerntool zu Berechnung unbekannter Winkel
Unser Lernvideo zu : Berechnung unbekannter Winkel
Vorgehen
![]()
Wir wollen diese Formel nach α umformen. Dazu benutzen wir Arkussinus. Arkussinus hebt links den Sinus auf. Links bleibt also nur noch α stehen. Rechts müssen wir Arkussinus von a/c berechnen. Wir erhalten:
![]()
Genauso funktioniert es auch mit Kosinus und Arkuskosinus bzw. Tangens und Arkustangens.
Beispiel
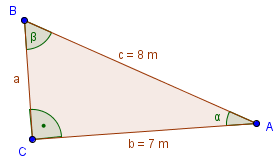
Berechne die fehlenden Winkel.
Berechnung von β
Wir können uns einen Winkel aussuchen, mit dem wir beginnen. Wir beginnen mit β. Wir benötigen also eine Formel in der nur β unbekannt ist. Da wir nur zwei Seiten gegeben haben, kommt nur der Sinus von β in Frage.
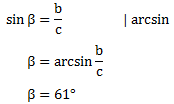
Berechnung von α
Es fehlt nun noch der Winkel α. Diesen können wir auf zwei Wegen berechnen:
Berechnung mithilfe der Trigonometrie
Zwar ist dies der etwas kompliziertere Weg, da wir aber gerade das Thema Trigonometrie haben, stellen wir diesen Weg als erstes vor. Da der alternative Weg auch nur funktioniert, wenn wir die anderen Winkel im Dreieck bereits kennen, müssen wir auch den Weg über die Trigonometrie beherrschen.
Da wir weiterhin nur zwei Seiten des Dreiecks kennen, müssen wir um α zu bestimmen mit dem Kosinus rechnen.
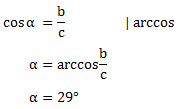
Berechnung mithilfe der Winkelsumme im Dreieck
Da wir schon zwei Winkel des Dreiecks kennen und wissen, dass die Winkelsumme im Dreieck immer 360° beträgt, können wir den letzten Winkel auch über eine einfache Subtraktion berechnen. Auch wenn wir den Winkel schon mithilfe der Trigonometrie berechnet haben, kann man das Ergebnis mit dieser Methode überprüfen.
![]()
Die 90° sind von dem rechten Winkel. Die 61° sind gleich β. Das Ergebnis ist natürlich auch hier α=29°.
