Konvexe, konkave und überschlagene Vierecke
Jedes Viereck hat zwei Diagonalen. In einer ebenen Figur ist eine Diagonale eine Verbindung von zwei nicht nebeneinander liegenden Ecken. Das bedeutet in einem Viereck werden die sich gegenüberliegende Ecken durch Diagonalen verbunden und es gibt somit zwei Diagonalen in jedem Viereck.
Konvexes Viereck
Liegen die Diagonalen beide innerhalb eines Vierecks, nennt man das Viereck konvex. Diese konvexen Vierecke sind die im Allgemeinen die normalen oder klassischen Vierecke.
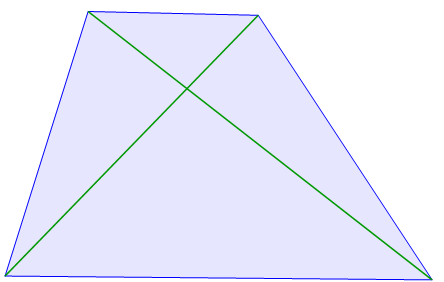
In dieser Abbildung sind man ein konvexes Viereck. Beide Diagonalen, grün eingezeichnet, sind innerhalb des Vierecks.
Konkaves Viereck
Liegt genau eine der beiden Diagonalen eines Vierecks außerhalb der Figur, dann handelt es sich um ein konkaves Viereck.
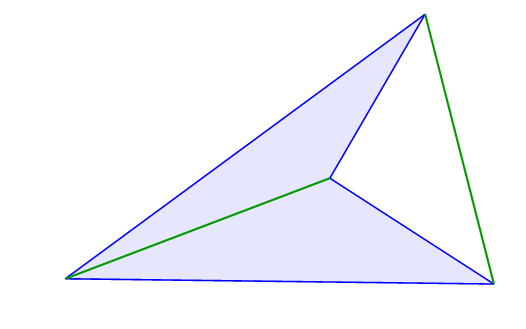
Hier seht ihr ein konkaves Viereck. Auch dieses Viereck hat zwei Diagonalen, allerdings liegt eine Außerhalb des Vierecks.
Überschlagenes Viereck
Wie der Name bereits verrät, überschlagen sich die Seiten eines überschalgenes Viereck. Bei einem solchen Viereck liegen beide Diagonalen außerhalb des Vierecks.
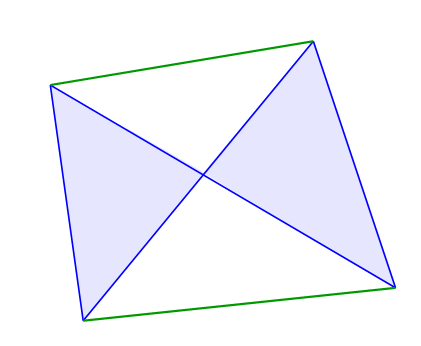
In der obigen Abbildung finden wir ein Viereck. Zwei Seiten des Viereck kreuzen sich. Dieses nennt man ein überschlagenes Viereck. Die beiden grünen Diagonalen liegen außerhalb des Vierecks.
