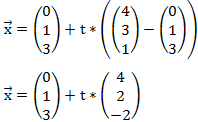Geraden im Raum
Die Beschreibung einer Geraden ähnelt einer Ebene in Parameterform. Eine Gerade sieht folgendermaßen aus:
Deutlicher wird das Ganze wenn wir ein Beispiel betrachten.
2D Beispiel
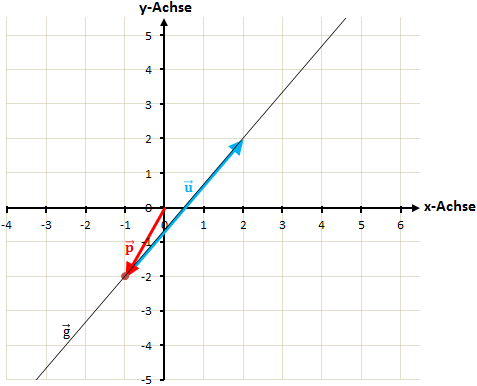
Gegeben ist folgende Gerade:
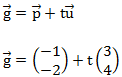
Der Vektor ![]() gibt einen Punkt auf der Geraden an. Der Vektor
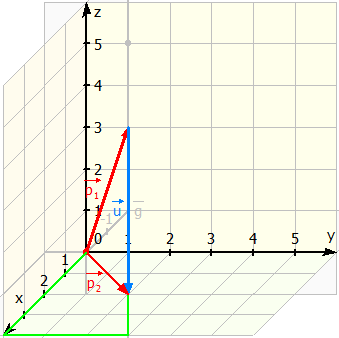
gibt einen Punkt auf der Geraden an. Der Vektor ![]() gibt dann die Richtung der Geraden an. Die Gerade sieht dann folgendermaßen aus:
gibt dann die Richtung der Geraden an. Die Gerade sieht dann folgendermaßen aus:
3D Beispiel
Bei der dritten Dimension bleibt alles genauso wie bei der Geraden im zweidimensionalen Raum. Die Dritte Koordinate wird einfach dazu geschrieben.
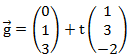
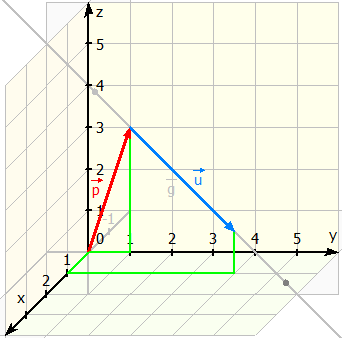
Und so sieht diese Gerade aus:
Unser Lernvideo zu : Geraden im Raum
Gerade durch zwei Punkte
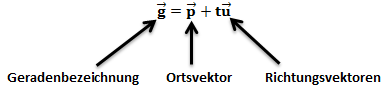
Um eine Gerade durch zwei Punkte zu berechnen müssen wir folgende Formel anwenden:
![]()
Einen Punkt können wir also direkt als Stützvektor benutzen. Der Richtungsvektor ist der Vektor von Punkt 1 zu Punkt 2.
Beispiel
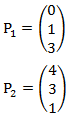
Wir setzen die beiden Punkte in die Formel ein und berechnen so die Gerade.