Partielle Integration
Die Formel für die Partielle Integration lautet:
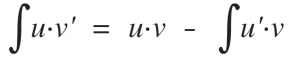
►Bei der partiellen Integration leitest du einen Teil der Funktion ab, während du vom anderen Teil die Stammfunktion bildest.
►Du kannst frei wählen, welche der beiden Teilfunktionen du jeweils auf- beziehungsweise ableiten möchtest.
►Der Name „partielle Integration“ kommt daher, dass zwar ein Teil der Funktion sofort integriert wird, aber gleichzeitig ein neues Integral entsteht, das man erst in einem zweiten Schritt lösen muss.
►Mit Hilfe der partiellen Integration können nicht nur bestimmte Integrale, sondern auch unbestimmte Integrale berechnet werden. Dann entfallen einfach die Integrationsgrenzen a und b. Du musst dann allerdings, wie bei allen unbestimmten Integralen, noch „+ C “ beim Ergebnis dazu schreiben.
►Eine Stammfunktion existiert, soweit die gegebene Funktion stetig ist, immer, ist aber nie eindeutig bestimmt.
Es gibt eine einfache aber hilfreiche Faustregel die du ebenfalls bei deiner Rechnung anwenden kannst. Es ist die LIATE Regel!
- L = logarithmische Funktionen (loge, loga, …)
- I = inverse Winkelfunktionen (asin, acos, atan, asec, …)
- A = algebraische Funktionen (x², 5x³, …)
- T = trigonometrische Funktionen (sin, cos, tan, csc)
- E = Exponentialfunktionen (ex, 5ax)
⇒Die Partielle Integration wird auch Produktintegration genannt.
Vorgehensweise:
- Wähle u und v‘
- Bilde damit u‘ und v
- Setze dies in die Formel ein
- Vereinfache deine Rechnung
- Löse das neu entstandene Integral
- Fasse die Lösung zusammen
Beispiel
Wir haben die folgende Funktion
![]()
⇒Wir bestimmen nun f(x) und g(x)
⇒f(x)= ex und g(x)= x2
⇒Jetzt bilden wir jeweils die Ableitungen f`(x)= ex und g`(x)=2x
⇒ Jetzt setzen wir in die Formel ein
![]()
und erhalten e – 2 ≈ 0,718 als Ergebnis!
