Fläche mit Vorzeichenwechsel
Bei der Integration ist zu prüfen, ob sich die berechnete Fäche vollständig auf einer Seite der x-Achse befindet. Sollte dies nicht der Fall sein, so muss die Integration jeweils an den Nullstellen unterteilt und die Beträge der Teilflächen addiert werden.
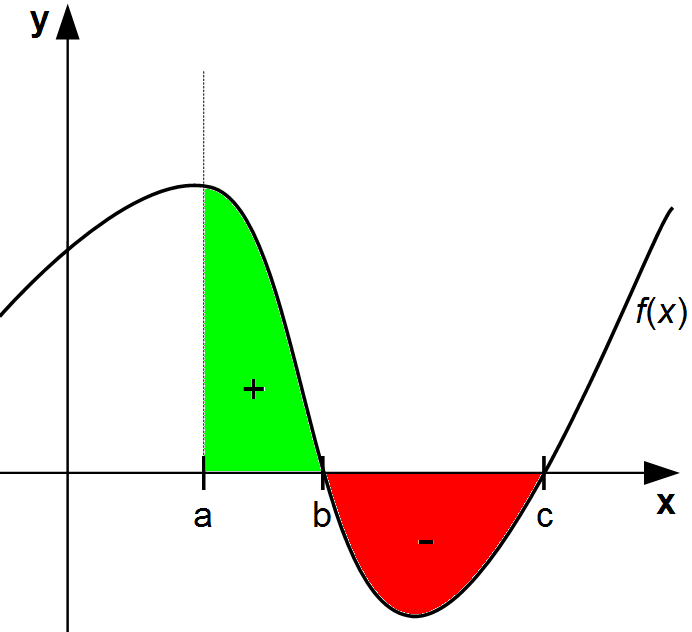
Einfacher gesprochen bedeutet dies, dass man bei den Flächen oberhalb der x-Achse einen positiven Wert und bei denen unterhalb der x-Achse einen negativen Wert erhält. Betrachtet man diese Teilfächen nicht getrennt, so bestimmt man lediglich die Summe an Teilflächen mit unterschiedlichen Vorzeichen und als Konsequenz einen kleineren als den gesuchten Flächeninhalt.
Stattdessen bestimmt man die Nullstellen der Funktion und unterteilt daraufhin die Fläche in entsprechende Teilflächen. Anschließend werden die Beträge dieser Teilflächen aufsummiert. Der Betrag wird mit senkrechten Strichen um den betrachteten Wert gekennzeichnet und beschreibt dessen Abstand zu Null. Das bedeutet, jede negative Zahl wird durch den Betrag positiv und jede positive Zahl bleibt unverändert. Mathematisch ausgedrückt sieht die Fläche dann folgendermaßen aus:
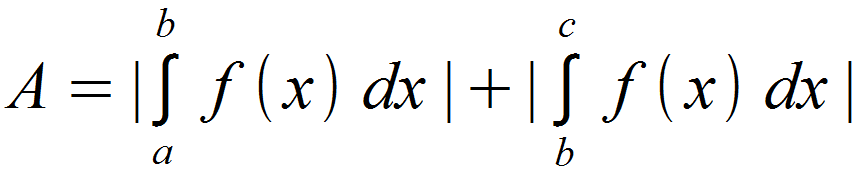
In der Formel ist beispielhaft nur der Fall für zwei Teilflächen aufgeführt, da im Intervall [a ; c] nur eine Nullstelle bei x = b vorliegt. Theoretisch können natürlich beliebig viele Teilflächen notwendig sein, von denen jeweils die Beträge aufsummiert werden müssen.
Unser Lernvideo zu : Fläche mit Vorzeichenwechsel
Beispiel
Die Fläche zwischen der Funktion f (x) = 2 x – 4 und der x-Achse soll für den Intervall [-6 ; 8] bestimmt werden.
Die Funktion f (x) beschreibt eine Gerade mit der Steigung 2. Sie schneidet die x-Achse bei 2, wodurch an dieser Stelle ein Vorzeichenwechsel vorliegt. Unterhalb der Nullstelle x = 2 nimmt die Funktion negative y-Werte an, oberhalb davon sind sie positiv.
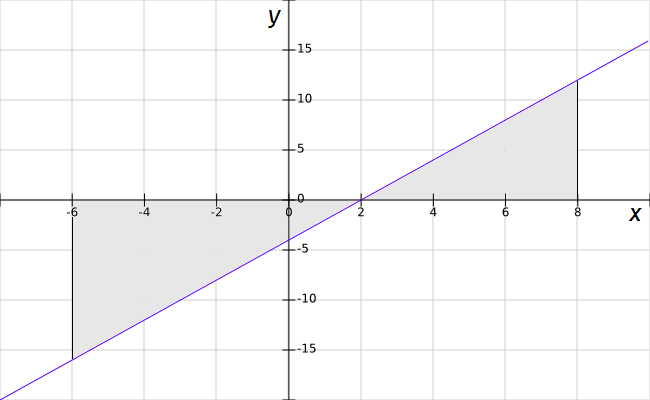
Würden wir jetzt stumpf das Integral von -6 bis 8 über diese Funktion berechnen, erhielten wir ein Ergebnis, dass sich aus einem negativen Wert für den Intervall von -6 bis 2 und einem positiven Wert für den Intervall von 2 bis 8 zusammensetzt. Wenn wir aber die Fläche zwischen der Gerade und der x-Achse wissen wollen, ist dies nicht der gesuchte Wert. Wir können aber den unteren Teil bis zur Nullstelle berechnen und davon den Betrag nehmen, also aus dem negativen Vorzeichen ein positives machen. Wenn wir noch den Wert oberhalb der Nullstelle addieren, erhalten wir die gesuchte Gesamtfläche A.
Gehen wir zunächst davon aus, uns lägen keine Informationen über die zu untersuchende Funktion vor. Dann ist der erste Schritt das Prüfen auf Nullstellen innerhalb des Intervalls, für den die Fläche bestimmt werden soll.
- Nullstellen bestimmen
Falls dir dies noch Probleme bereiten sollte, findest du im Kapitel Nullstellen (Grundlagen) Abhilfe. Wir setzen die Funktion gleich Null und lösen nach x auf.
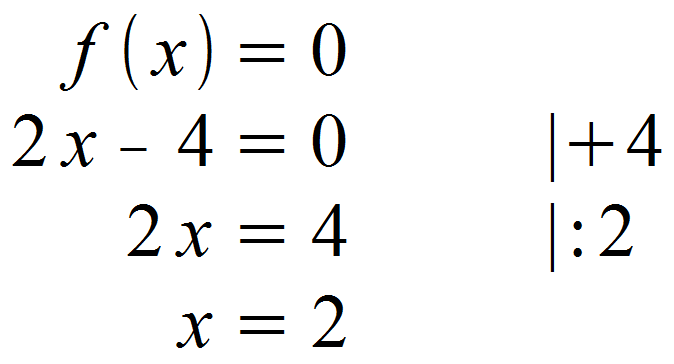
Es liegt also eine Nullstelle bei x = 2 vor. Diese Nullstelle liegt innerhalb unseres Intervalls [-6 ; 8] und wir müssen die zu berechnende Fläche somit unterteilen.
- Gleichung für die Fläche aufstellen
Der betrachtete Intervall beginnt bei x = -6 und endet bei x = 8, die Nullstelle liegt bei x = 2. Dementsprechend teilen wir in zwei Teilflächen auf und schreiben:
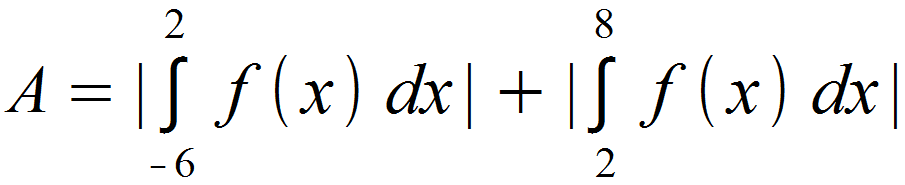
- Teilflächen berechnen
Wir lösen hier zunächst das Integral unterhalb der Nullstelle. Dafür integrieren wir zunächst die Funktion und setzen daraufhin die Integrationsgrenzen -6 und 2 in die Stammfunktion F (x) = x2 – 4 x ein.
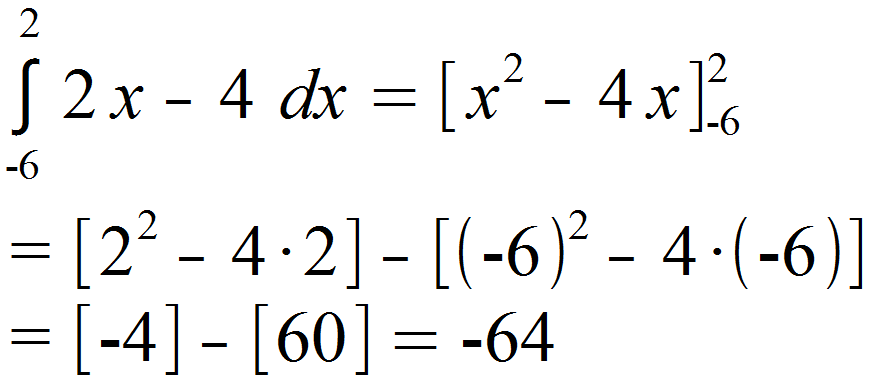
Ebenso verfahren wir für das Integral oberhalb der Nullstelle. Hierbei ändern sich lediglich die Integrationsgrenzen, der Weg bleibt der gleiche.
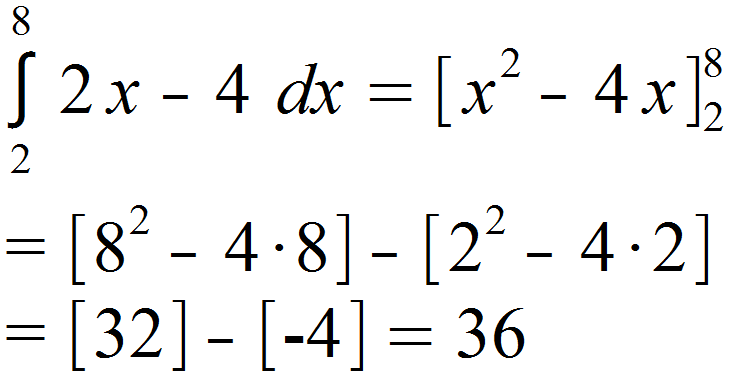
- Fläche berechnen
Mit den gelösten Integralen können wir jetzt abschließend die Fläche bestimmen.
![]()
