Kommutativgesetz
Das Kommutativgesetz gilt für die Addition und Multiplikation. Es besagt, dass man die Summanden der Addition und die Faktoren der Multiplikation vertauschen darf und trotzdem das gleiche Ergebnis erhält.
Addition
Für die Addition bedeutet dies folgendes:
a + b = b + a
a und b sind dabei Variablen, die beliebige Werte annehmen dürfen. Man kann also sowohl a + b als auch b + a rechnen, ohne dass sich das Ergebnis verändert.
Das Ganze noch einmal mit eingesetzten Zahlen:
3 + 8 = 11 und
8 + 3 = 11
Wie eben erklärt sehen wir hier, dass wir die Reihenfolge der Summanden tatsächlich vertauschen können. Es ist egal, ob wir 3 + 8 oder 8 + 3 rechnen. Wir erhalten immer als Ergebnis 11.
Diese Regel ist unabhängig von der Anzahl der Summanden! Egal wie viele Summanden addiert werden sollen, sie können in beliebiger Reihenfolge berechnet werden.
4 + 8 + 9 + 3 = 24 und
3 + 9 + 4 + 8 = 24 und
8 + 4 + 9 + 3 = 24
Multiplikation
Das Kommutativgesetz gilt auch für die Multiplikation:
a · b = b · a
Wie zu sehen ist es auch hier egal, in welcher Reihenfolge wir die Faktoren multiplizieren.
Beispiel:
3 · 8 = 24 und
8 · 3 = 24
Wenn wir 3 mit 8 multiplizieren, erhalten wir dasselbe Ergebnis wie bei der Multiplikation von 8 mit 3.
Das Ganze geht natürlich auch hier mit beliebig vielen Faktoren.
4 · 2 · 9 · 10 = 720 und
9 · 4 · 10 · 2 = 720
Unser Lernvideo zu : Kommutativgesetz
Rechenvorteile
Das Kommutativgesetz bringt den Vorteil, dass man selber überlegen kann, welche Faktoren oder Summanden man als erstes Rechnen möchte. Manchmal ergeben sich dadurch Rechenvorteile.
Beispiel
42 + 33 + 67 = 142
Wenn wir einfach von links nach rechts vorgehen, rechnen wir 42 + 33 = 75 und anschließend addieren wir 67, Also 75 + 67 = 142.
Ein bisschen leichter ist es allerdings, wenn wir die Reihenfolge vertauschen:
Wir rechnen zuerst 33 + 67 = 100, da wir hier die Zehnerstellen glatt auffüllen können. Und addieren anschließend 42. 100 + 42 = 142.
Das Ergebnis ist in beiden Fällen dasselbe. Der Weg dorthin ist allerdings im zweiten Fall ein wenig einfacher.
33 + 67 + 42 = 142
Kommutativgesetz nicht anwendbar
Für die Subtraktion und die Division gilt das Kommutativgesetz nicht. Hier ist es wichtig, in welcher Reihenfolge wir die Zahlen oder Variablen schreiben.
Beispiel für die Subtraktion:
5 – 3 = 2 ≠ 3 – 5 = -2
Wir sehen hier deutlich, dass es nicht egal ist, in welcher Reihenfolge wir Minuend (die Zahl, von der wir abziehen) und Subtrahend (die Zahl, die abgezogen wird) schreiben.
Beispiel für die Division:
10 : 2 = 5 ≠ 2 : 10 = 0,2
Auch bei der Division gilt das Kommutativgesetz nicht. Wir dürfen Dividend (die Zahl, die geteilt wird) und Divisor (die Zahl, durch die geteilt wird) nicht vertauschen!
Gemischte Addition und Multiplikation
Das Kommutativgesetz gilt also nur bei der Addition und Multiplikation. Wir dürfen aber nur bei reiner Addition oder reiner Multiplikation die Reihenfolge vertauschen. Wenn Addition und Multiplikation vermischt auftreten, gilt dies nur für die Teile reiner Addition oder Multiplikation. Man muss also gut aufpassen, welche Teile man vertauscht und welche nicht.
Beispiel
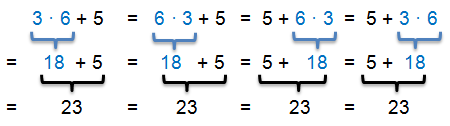
Wir dürfen aber nicht schreiben: 5 · 3 + 6, denn das ergibt: 21
3 · 6 stellt eine Multiplikation dar, dessen Faktoren wir vertauschen können (3 · 6 = 6 · 3). Das Ergebnis von 3 · 6 (bzw. von 6 · 3) wird mit 5 addiert. Die Summanden der Addition wären hier also 3 · 6 und 5. Diese können wir auch vertauschen. 3 · 6 + 5 = 5 + 3 · 6.
Interessante Fragen und Antworten zu Kommutativgesetz
„Zeige allgemein, dass die Matrixmultiplikation nicht kommutativ ist.“ Wie mache ich das? |
| Die Frage die sich aus dem Kommutativgesetz ergeben kann; „Zeige allgemein, dass die Matrixmultiplikation nicht kommutativ ist.“ und die Beantwortung wie man diese Berechnung widerlegen kann ist sehr einfach zu beantworten. Man kann zunächst direkt versuchen das Gegen Beispiel auszurechnen und das diese Aussage damit wiederlegen.Wie sicher ist aber diese einfache Methode un bestimmt Sie wirklich die Aussage, dass die Multiplikation der Matrix nicht kommutativ ist? an merkt also es ergeben sich Zweifel, jedoch ist hier in der Mathematik der Weg wirklich einfach und das Gegen Beispiel reicht wirklich aus.
Der Grundsatz lautet dazu, dass Multipliaktionen von mindestens zweimal einer Matrix immer kommutativ sind. Beispiel der Matrix in der Mehrzahl mit A x B = B x A. Es erscheint unmöglich dass diese Feststellung immer falsch ist und die Matrix A * B = B * A kann erweitert werden. Würde man also zweimal diese Matrix berechnen, dann ist der Grundsatz widerlegt. Ein weiterer Grundsatz zur Beantwortung dieser Frage lautet; damit man zweimal eine Matrix multiplizieren kann, muss immer die Zahl der Spalten der der ersten Matrix mit der Zahl der Zeilen der zweiten Matrix identisch sein. Grundsätzlich ist das Ergebnis dann widerum eine Matrix und damit kommutativ. Die Ergebnisse dieser Berechnungen werden mit den Begriffen der Matrix Berechnung, als Matrixprodukt oder nur Produkt Matrix benannt. |
Wie lässt sich das Kommutativgesetz auf die Matrix Multiplikation übertragen? |
| Die Matrix Multiplikation oder auch Matritzenmultiplikation ist das Ergebnis der Multiplikation zweier Matritzen miteinander. Allgemein gilt, dass das Kommutativgesetz nicht auf eine Matrix anwendbar ist. Das stimmt jedoch nur zum Teil. Wichtige Voraussetzung, damit das Kommutativgesetz auch auf zwei Matritzen anwendbar ist, ist allerdings, dass die Anzahl der Spalten von der ersten Matrix mit der Anzahl der Zeilen von der zweiten Matrix übereinstimmt. Ist dies der Fall, so ist das Ergebnis eine neue Matrix mit der Anzahl der Zeilen der ersten Matrix und der Anzahl der Zeilen der zweiten Matrix die wir miteinander multipliziert haben. Sehen wir uns nun das Schema an, wie eine Matrix Multiplikation funktioniert: Es wird nämlich das Schema Zeile mal Spalte angewendet. Das Ergebnis dieser Multiplikation ist dann eine Matrix mit der gleichen Anzahl an Spalten wie die der ersten Matrix und die exakt gleiche Anzahl an Zeilen wie die der zweiten Matrix. Wenn dies gilt, so kann man durchaus auch die Matritzen miteinander vertauschen, also das Kommutativ-Gesetz anwenden. Denn die neue Matrix setzt sich zusammen aus Spalten mal Zeilen. Diese binäre Gleichung ist dann wiederum eine ganz normale Multiplikation aus a x b, welche dann auch umgeformt werden darf in b x a. Lediglich die Abbildung der Ergebnis-Matrix ist eine andere. |
