Funktionsschar
Wir haben die folgende Funktion gegeben. Unser Funktionsschar lautet fa(x) = x2 + (1-2a)x – 2a
Berechnen wollen wir folgendes
- Nullstelle
- Extrempunkt
- Wendepunkt
f(x) = x2 + (1 – 2a)·x – 2a
f'(x) = 2x – 2a + 1 ►1. Ableitung
Nullstellen f(x) = 0
x2 + (1 – 2a)·x – 2a = 0
► lösen nach x auf und erhalten als Nullstelle: x1 = 2a und x2 = -1
Extrempunkt f'(x) = 0
2x – 2a + 1 = 0
x = a – 1/2
f(a – 1/2) = – a2 – a – 1/4 ► Da die Funktion eine nach oben geöffnete Parabel ist, ist das ein Tiefpunkt. Wendepunkte gibt es bei der Parabel nicht.
anderes Beispiel
Funktionsschar fz(x) = x3 – 3zx2 + (3z2 – 4)x – z3 + 6z
berechnen wollen wir folgendes: Wendepunkt
Zuerst bilden wir die ersten beiden Ableitungen.
f(x) = x3 – 3·z·x2 + (3·z2 – 4)·x – z3 + 6·z ► Funktion
f'(x) = 3·x2 – 6·z·x + 3·z2 – 4 ► 1. Ableitung
f“(x) = 6·x – 6·z ►2 Ableitung
Bedingung für die Wendestelle f“(x) = 0
6·x – 6·z
z = x
►Ich setzte für z in die ursprüngliche Funktion x ein
y = x3 – 3·x·x2 + (3·x2 – 4)·x – x3 + 6·x = 2·x
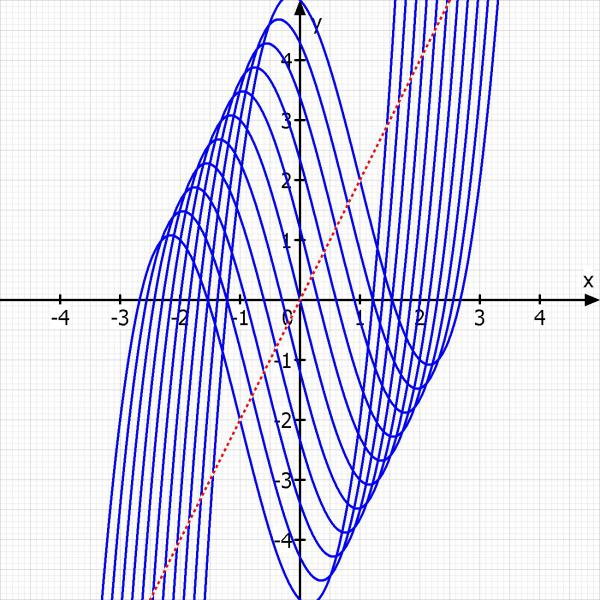
info :►Wir haben eine Wendestelle bei x, wenn z = x. Wenn man diese Bedingung in die Originalfunktion für z einsetzt bekommt man die Ortskurve aller Wendepunkte. Das gilt allgemein so.
Merke
- Funktionssharen können einen, aber auch mehrere Parameter besitzen
- Hat eine Kurvenshar nur einen einzigen Sharparameter, spricht man von einer einparametrigen Kurvenshar; bei zwei Sharparametern entsprechend analog von einer zweiparametrige Kurvenshar, usw.
- Kurvensharen haben mindestens einen Merkmal gemeinsam. Dies kann beispielsweise ein gemeinsamer Schnittpunkt oder Form sein
- Ist die Funktion linear, spricht man auch von einer Geradenschar.
- der Parameter kann verschiedene Werte annehmen
