Wurzelgesetze
Mit Wurzeln rechnen zu können, muss man üben. Erst einmal muss man aber die Regeln dafür kennen. Wir wollen hier einen Überblick über die wichtigsten Wurzelgesetze geben.
Addition und Subtraktion
Addition
Wenn wir zwei Wurzeln addieren, besteht die Frage, ob wir diese weiter zusammenfassen, also unter ein Wurzelsymbol schreiben können.
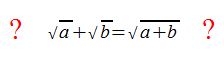
Beispiel für Addition:
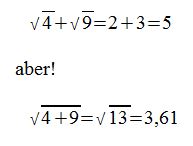
Daraus folgt:
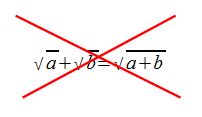
Bei der Addition können wir die Wurzeln nicht zusammenfassen!!!
Subtraktion
Nun schauen wir uns die Subtraktion von zwei Wurzeln an. Und wollen wieder wissen, ob wir die Wurzeln zusammenfassen können:
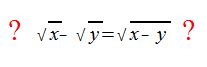
Beispiel für Subtraktion:
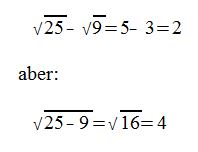
Daraus folgt:
Auch bei der Subtraktion können wir die Wurzeln nicht zusammenfassen!
Unser Lernvideo zu : Wurzelgesetze
Multiplikation und Division von gleichnamigen Wurzeln
Was können wir machen, wenn gleichnamige Wurzeln multipliziert oder dividiert werden. Dies schauen wir uns nachfolgend mit Beispielen an.
Multiplikation von gleichnamigen Wurzeln
Ist folgende Aussage richtig?
![]()
Beispiel:
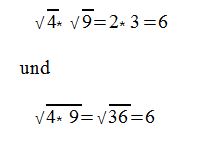
Daraus folgt:
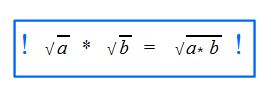
Wir können die Wurzel bei der Multiplikation also über jede Variable einzeln schreiben oder auch über alle zusammen, je nachdem was für uns gerade besser ist.
Division von gleichnamigen Wurzeln
Ist folgende Aussage über die Division von Wurzeln richtig?
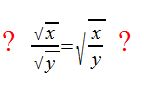
Beispiel:
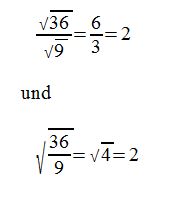
Daraus folgt:
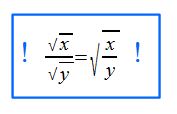
Auch bei der Division können wir die Faktoren unter einer Wurzel setzen und erhalten in beiden Fällen dasselbe Ergebnis.
Mutliplikation und Divison von ungleichnamigen Wurzeln
Bei den gleichnamigen Wurzeln konnten wir feststellen, dass eine Multiplikation und Division von Wurzeln funktioniert. Nun zeigen wir, wie das bei ungleichnamigen Wurzeln, also Wurzeln, die nicht den gleichen Wurzelexponenten haben, berechnet wird.
Multiplikation von ungleichnamigen Wurzeln
Problematik: ![]()
Wir haben hier zwei Wurzeln mit unterschiedlichem Wurzelexponenten, also ungleichnamig. Diese können wir nicht wie die gleichnamigen Wurzeln unterm Wurzelstrich addieren, sondern müssen zunächst einige Vorraussetzungen schaffen.
Dazu sind 3 Schritte notwendig: a) das kleinste gemeinsame Vielfache (kgV) der Wurzelexponenten finden
b) die Wurzeln erweitern
c) dann multiplizieren
Beispiel 1:
![]()
a) kgV finden:
kgV (2,3) = 6
b) die Wurzeln erweitern:
wenn man den kgV ermittelt hat, wird die Wurzel um den fehlenden Faktor erweitert. Dazu wird der Wurzelexponent multipliziert und der Radikant wird mit dem gleichen Faktor potenziert. So verändern wir das Ergebnis nicht, sondern drücken es nur anders als, ähnlich wie beim Bruchrechnen.
In diesem Fall wird die erste Wurzel mit 3 erweitert und die zweite mit 2. Wir erhalten folgendes:
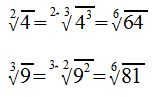
c) multiplizieren:
die eben erweiterten Wurzeln sind nun gleichnamig und können wie bekannt multipliziert werden.
![]()
Beispiel 2:
![]()
a) kgV finden:
kgV (4,3) = 12
b) erweitern der Wurzeln
![]()
c) multiplizieren:
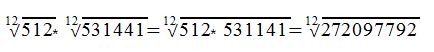
Wie an den beiden Beispielen zu sehen, können wir nach erweitern der Wurzeln diese multiplizieren.
Division von ungleichnamigen Wurzeln
Problematik: 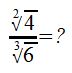
Es besteht die Problematik darin, dass wir nicht wie bei gleichnamigen Wurzeln die Divsion direkt unter einer gesamten Wurzel schreiben können. Auch hier müssen wir zunächst die Wurzeln gleichnamig machen und können sie erst dann zusammenfassen.
Beispiel 1:
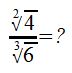
a) kgV finden:
kgV (2,3) = 6
b) erweitern der Wurzeln:

c) dividieren:
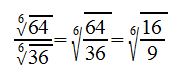
Beispiel 2:
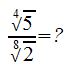
a) kgV finden:
kgV (4,8) = 8
b) erweitern der Wurzeln
![]()
c) dividieren:
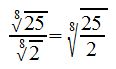
Die Beispiele zeigen, dass wir durch das Erweitern die nun gleichnamigen Wurzeln dividieren können, so wie wir es bereits oben erfahren haben.
Negative Quadratwurzeln
Aus einer negativen Zahl die Quadratwurzel ziehen, geht nicht. Dies liegt daran, dass die Wurzel für negative Zahlen nicht definiert ist. Aber warum ist das so?
Die Wurzel ist die Umkehrfunktion von dem Quadrat. Wenn wir eine Zahl quadrieren (²), kommt immer eine positive Zahl raus. Niemals aber eine negative. Das ist der Grund, warum wir auch aus einer negativen Zahl keine Wurzel ziehen können.
Die n-te Wurzel
Die „normale“ Wurzel nennt man Quadratwurzel (oder zweite Wurzel). Man kann sie auch mit einer 2 schreiben:
![]()
Die Bedeutung ist genau dieselbe. Bei dieser Rechnung ziehen wir die zweite Wurzel, was die Umkehrung vom Quadrieren ist.
Nun wissen wir, dass man nicht nur hoch 2, sondern auch mal hoch 3, hoch 4, usw rechnet. Auch dafür muss es eine Umkehrung geben, Dies nennt sich die die n-te Wurzel. man schreibt:
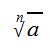
Dies sagt aus, dass die Zahl b mit n potenziert a ergibt:
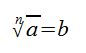
Beispiel 1:
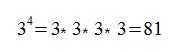
um dies zurückrechnen zu können, müssen wir die 4te Wurzel aus 81 ziehen. Wir schreiben:
![]()
Beispiel 2:
![]()
Wurzelberechnung:
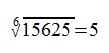
Wir merken uns:
![]()
Interessante Fragen und Antworten zu Wurzelgesetze
Was bedeutet kgV? |
| Bei den Mathematischen Wurzelgesetzen gibt es den Begriff kgV, der sich wie folgt definiert;Schon an den Buchstabenfolge ist erkennbar, dass es sich um das -kleinste gemeinsame Vielfache- handelt. Das ist das Pendant zum größten gemeinsame Teiler. Beide Begriffe sind maßgeblich wichtig für die Berechnungen der Brüche. Diese Begriffe sind wichtig bei Bruchrechnungen. Sie sind bestimmend in der Theorie der immer wiederkehrenden Zahlen und eines entsprechenden statistischen vorkommenden Mechanismus.
Das kgV ist bestimmbar und nennt das Vielfache zweier ganzer Zahlen. Es ist immer eine natürliche Zahl. Alle natürlichen Zahlen sind beispielsweise die 1, 2, 3 usw. und auch in bestimmten Fällen wird die 0 als natürliche Zahl bezeichnet. Das kgV ergibt sich aus der Rationalität und der entsprechenden Berechnung. 1 x 1 = 1 . Dies ist das einfachste Beispiel und geht man dazu in der Zahlenfolge weiter kann man immer diese Rechenformel dazu anwenden und die entsprechende Berechnung der Brüche einbeziehen. |
