Umrechnung Parameterform – Normalenform
Parameterform in Normalenform
Um von der Parameterform zu der Normalenform zu gelangen, benötigt man nur den Normalenvektor ![]() der Ebene. Der Orts- bzw. Stützvektor
der Ebene. Der Orts- bzw. Stützvektor ![]() bleibt der Gleiche.
bleibt der Gleiche.
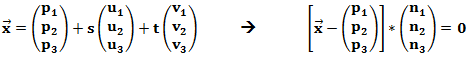
Wir müssen aus den Vektoren ![]() und
und ![]() den Vektor
den Vektor ![]() berechnen. Wir müssen also den Normalenvektor der Ebene berechnen. Wie wir diesen berechnen haben wir bereits im Kapitel „Normale einer Ebenen“ beschrieben. Wir zeigen die Umrechnung hier noch einmal anhand eines Beispiels. Die Parameterform lautet:
berechnen. Wir müssen also den Normalenvektor der Ebene berechnen. Wie wir diesen berechnen haben wir bereits im Kapitel „Normale einer Ebenen“ beschrieben. Wir zeigen die Umrechnung hier noch einmal anhand eines Beispiels. Die Parameterform lautet:
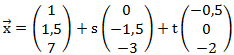
Wir müssen jetzt die Normale der Ebene berechnen. Dafür berechnen wir das Kreuzprodukt der beiden Richtungsvektoren.
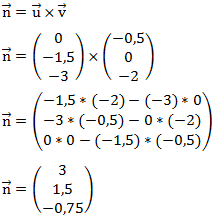
Die Normalenform für diese Ebene lautet also:
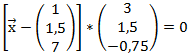
Unser Lernvideo zu : Umrechnung Parameterform – Normalenform
Normalenform in Parameterform
Um die Normalenform in die Parameterform umzurechnen, müssen wir denselben weg rückwärtsgehen. Wir müssen also aus dem Normalenvektor zwei Richtungsvektoren berechnen, welche die Ausrichtung der Ebene beschreiben. Dabei ist es wichtig, dass die beiden berechneten Vektoren linear unabhängig (also nicht parallel) sind, da sie sonst keine Ebene aufspannen können.
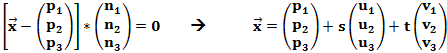
Beispiel
Wir nehmen die Normalenform des vorhergehenden Beispiels und formen diese wieder zurück in die Parameterform.
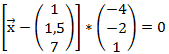
Wir müssen nun zwei Vektoren ![]() und
und ![]() finden, welche senkrecht zu dem Normalenvektor ausgerichtet sind. Das Skalarprodukt muss also 0 ergeben. Dies notieren wir in zwei Gleichungen:
finden, welche senkrecht zu dem Normalenvektor ausgerichtet sind. Das Skalarprodukt muss also 0 ergeben. Dies notieren wir in zwei Gleichungen:
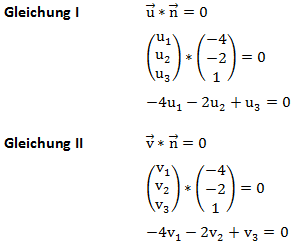
Wir haben also im Prinzip zweimal die gleiche Gleichung um ![]() und
und ![]() zu berechnen. In jeder Gleichung befinden sich außerdem 3 Unbekannte. Wir können die Gleichung also nur lösen indem wir uns zwei Werte frei aussuchen und dann den dritten berechnen. Wir wählen:
zu berechnen. In jeder Gleichung befinden sich außerdem 3 Unbekannte. Wir können die Gleichung also nur lösen indem wir uns zwei Werte frei aussuchen und dann den dritten berechnen. Wir wählen:
![]()
Bei den Werten für v müssen wir nun aufpassen, dass die Vektoren linear unabhängig werden. Wir dürfen also nicht – wie eben – dieselben Werte für ![]() und
und ![]() wählen. Wir wählen:
wählen. Wir wählen:
![]()
Wir setzen ein und berechnen:
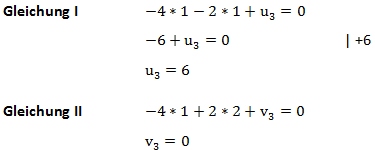
Die Beiden Vektoren sind also:
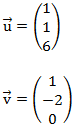
Die Parameterform lautet also:
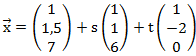
Jetzt kann man sich natürlich fragen, warum dieses Ergebnis so wenig mit der Ausgangsgleichung des vorherigen Beispiels zu tun hat. Dies liegt daran, dass es in der Parameterform unendlich viele verschiedene Vektoren gibt, die alle dieselbe Ebene beschreiben.

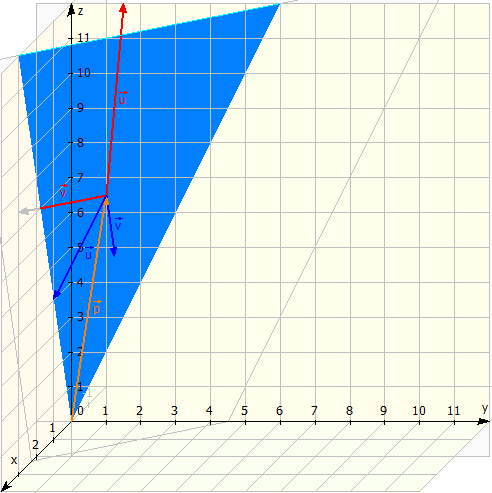
Wir schauen uns das Ganze noch einmal im 3D-Raum an. Die Vektoren sind dabei in den entsprechenden Farben dargestellt. Die roten und blauen Vektoren liegen dabei alle in der blau eingezeichneten Ebene und beschreiben damit genau dieselbe Ebene.