Umrechnung Koordinatenform – Parameterform
Von Koordinatenform zur Parameterform
Um von der Koordinatenform zu der Parameterform zu kommen, müssen wir uns am besten 3 Punkte suchen die in der Ebene liegen. Bei diesen drei Punkten muss die Koordinatengleichung also erfüllt sein. Aus einem der Punkte wird dann der Stützvektor ![]() . Aus den anderen beiden kann man die Richtungsvektoren
. Aus den anderen beiden kann man die Richtungsvektoren ![]() und
und ![]() berechnen.
berechnen.

Beispiel
Wir haben eine Ebene in der Koordinatenform gegeben:
![]()
Wir suchen nun drei Punkte welche in der Ebene liegen. Um diese zu finden, macht es Sinn, sich die x- und y-Koordinaten auszudenken und dann die z-Koordinate zu berechnen, sodass die Gleichung erfüllt ist.
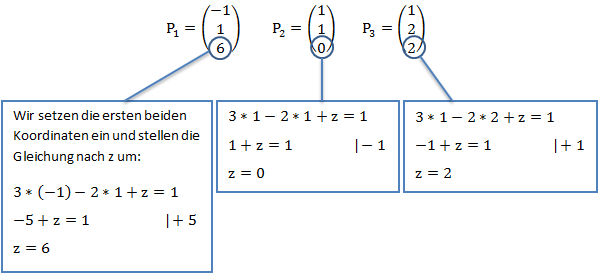
Die ersten beiden Koordinaten müssen jeweils unterschiedlich und keine vielfachen voneinander sein, da die Vektoren sonst linear abhängig sein könnten.
Aus einem der drei Punkte machen wir nun unseren Stützvektor ![]() . Wir nehmen dafür den Punkt 1:
. Wir nehmen dafür den Punkt 1:
![]()
Aus den anderen beiden Punkten berechnen wir die Richtungsvektoren ![]() und
und ![]() . Dafür berechnen wir die beiden Vektoren:
. Dafür berechnen wir die beiden Vektoren:
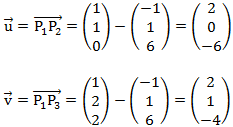
Der Vektor ![]() ist dabei der Vektor um vom Punkt 1 zu Punkt 2 zu gelangen und der Vektor
ist dabei der Vektor um vom Punkt 1 zu Punkt 2 zu gelangen und der Vektor ![]() wird benötigt um von Punkt 1 zu Punkt 3 zu kommen.
wird benötigt um von Punkt 1 zu Punkt 3 zu kommen.
Damit haben wir alle drei benötigten Vektoren und können die Ebene in Parameterform notieren:
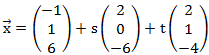
Unser Lernvideo zu : Umrechnung Koordinatenform – Parameterform
Von Parameterform zur Koordinatenform
Um von der Parameterform zur Koordinatenform zu kommen, geht man am besten den Umweg über die Normalenform. Wir werden hier also nur ein kurzes Beispiel geben. Das genau Vorgehen kann in den Teilen „von Parameterform zur Normalenform“ und „von Normalenform zur Koordinatenform“ nachgelesen werden.
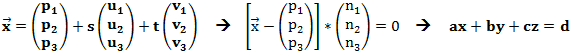
Beispiel
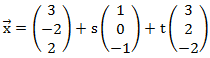
Um zu der Normalenform zu gelangen müssen wir das Kreuzprodukt der beiden hinteren Vektoren berechnen:
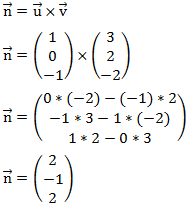
Damit sind wir bereits bei der Normalenform:
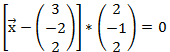
Um zu der Koordinatenform zu gelangen müssen wir nun noch ausmultiplizieren:
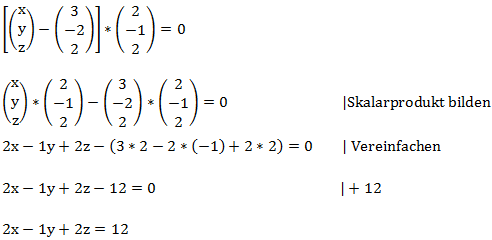
Damit ist die Umrechnung in die Koordinatenform abgeschlossen.
