Ebenen
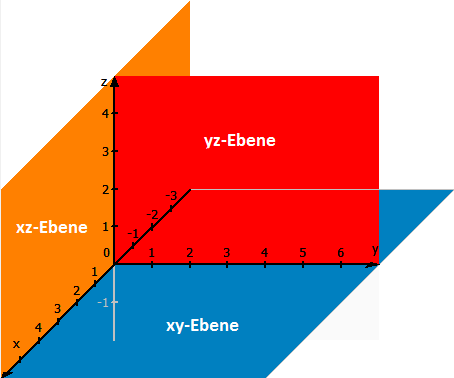
Eine Ebene ist im mathematischen Sinne ein flaches, ebenes Objekt. Die Ebene selbst hat dabei nur zwei Dimensionen, kann sich aber natürlich im dreidimensionalen Raum befinden. Typische Ebenen sind dabei die xy-, die xz- und die yz-Ebene. Die xy-Ebene ist dabei die Ebene, die durch die x und die y-Achse aufgespannt wird. Sie ist die Ebene die wir üblicherweise im 2D-Raum benutzen. Die xz-Ebene ist dementsprechend die Ebene die durch die x und z-Achse aufgespannt wird. Bei der yz-Ebene verhält es sich entsprechend. Auf der Zeichnung sind die Ebenen natürlich abgeschnitten dargestellt, theoretisch reichen sie jedoch unendlich weit.
Beschreiben von Ebenen
Natürlich gibt es aber auch andere Ebenen. Wir können eine beliebige Ebene definieren. Wir machen dies mithilfe von Vektoren. Wir brauchen dafür einen Ortsvektor (oder Stützvektor) und Richtungsvektoren. Im Prinzip unterscheiden sich diese nur in ihrer Funktion. Ein Ortsvektor beschreibt einen Ort im Koordinatensystem. Er geht vom Ursprung des Koordinatensystems aus. Ein Richtungsvektor hingegen beschreibt eine Richtung. Um eine Ebene aufzuspannen, benötigen wir einen Ortsvektor und zwei Richtungsvektoren. Die Richtungsvektoren spannen die Ebene auf und bestimmen die Ausrichtung. Der Ortsvektor sorgt für die gewünschte Verschiebung vom Ursprung.
Eine Ebenenbeschreibung kann folgendermaßen aussehen (Parameterform):
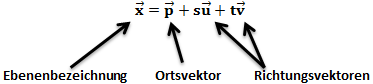
Eine Grundvoraussetzung hierfür ist, dass die beiden Richtungsvektoren linear unabhängig sind. Was das genau bedeutet, erklären wir in einem späteren Abschnitt.
Eine Ebene Zeichnen
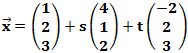
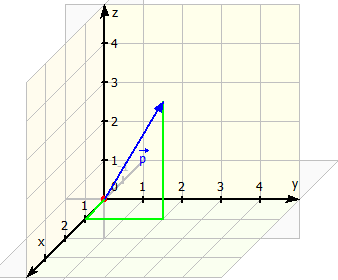
Mit 
wird die Ebene bezeichnet. Um die Ebene zu zeichnen, müssen wir zunächst einmal den Punkt einzeichnen, welcher von dem Ortsvektor beschrieben wird.
Anschließend zeichnet man die beiden Richtungsvektoren 
und 
ein. Dabei geht man von dem bereits eingezeichneten Vektor 
aus.
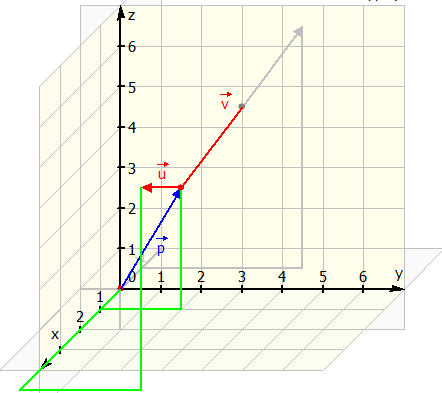
Jetzt haben wir alle Informationen die wir benötigen um die Ebene aufzuspannen. Mit der Hand ist es relativ schwierig, eine Ebene im drei dimensionalen Koordinatensystem einzuzeichnen, wir zeigen hier trotzdem wie diese Ebene aussehen würde.
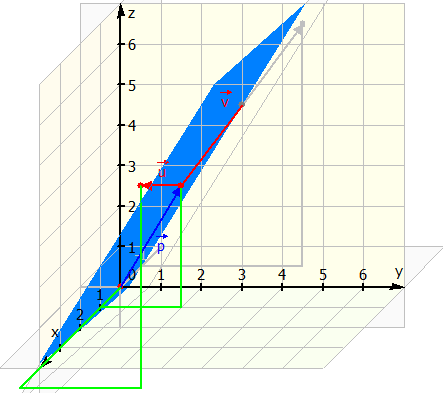
Was bedeuten die Parameter s und t
Um jeden Punkt auf der beschriebenen Ebene zu erreichen, benötigt man natürlich mehr als nur drei Vektoren. Deshalb sind den beiden Richtungsvektoren noch die Parameter s und t zugeordnet. Durch die Multiplikation der Vektoren mit einer beliebigen Zahl, ist es möglich, jeden Punkt auf der Ebene zu erreichen. Andersherum gehört jeder erreichbare Punkt zu der beschriebenen Ebene.