Abstand von Punkt zu Gerade
Ist nach dem Abstand zwischen einem Punkt und einer Geraden gefragt, so sucht man immer die kürzeste Verbindung zwischen beiden. Im zweidimensionalen Raum sieht das folgendermaßen aus:
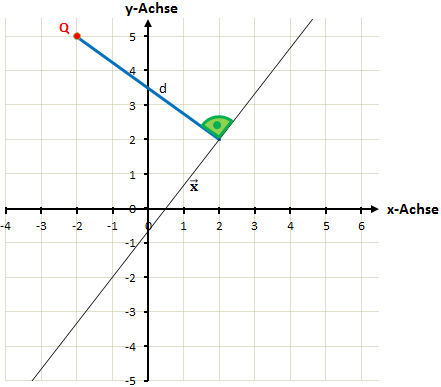
Zunächst soll das Vorgehen ohne konktrete Zahlenwerte erläutert werden. Das mag dich zunächst vielleicht irritieren, weshalb der Rechenweg weiter unten noch mit einem Beispiel verständlich gemacht wird. Gegeben sind also eine Geradengleichung g und ein Punkt Q, die wie folgt definiert sind:
![]()
Für die Formel müssen wir zunächst den Ortsvektor q zu unserem Punkt Q bilden.
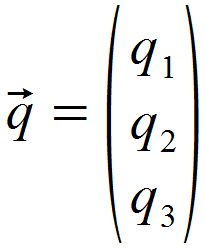
Mithilfe dieser Informationen kann jetzt der Abstand berechnet werden. Hierfür setzen wir im Nenner den Betrag des Richtungsvektors u unserer Geradengleichung ein. Für den Zähler bilden wir das Kreuzprodukt desselben Richtungsvektors u sowie der Differenz aus dem Ortsvektor q unseres Punktes und dem Ortsvektor p unserer Geradengleichung, von dem wir anschließend ebenfalls den Betrag nehmen.
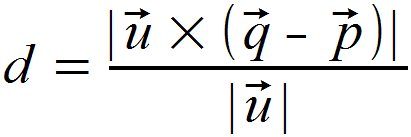

Für den Nenner muss das Kreuzprodukt zweier Vektoren gebildet werden, was du am „x“ erkennen kannst. Hierfür wird allgemein folgendermaßen vorgegangen:
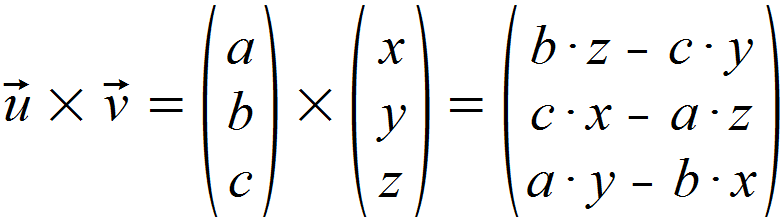
Der Betrag eines Vektors stellt dessen Länge dar. Er kann mit folgender Formel berechnet werden:
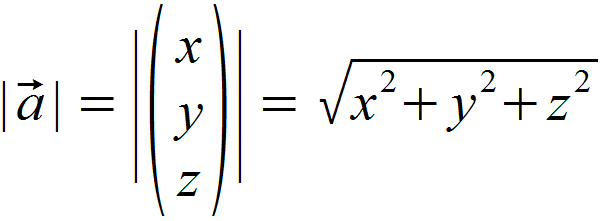
Unser Lernvideo zu : Abstand von Punkt zu Gerade
Beispiel
Es soll der Abstand zwischen der folgenden Geraden g sowie des Punktes Q bestimmt werden.
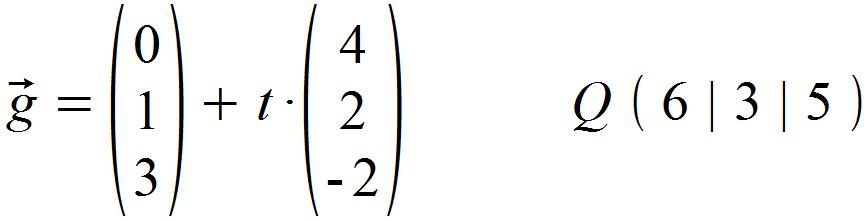
Lösung
Zunächst identifizieren wir alle nötigen Vektoren für unsere Formel.
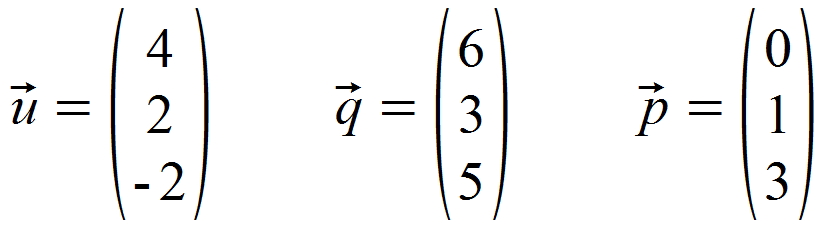
Der Übersicht halber berechnen wir Zähler und Nenner der Formel lieber getrennt und beginnen mit dem Zähler.
Zähler
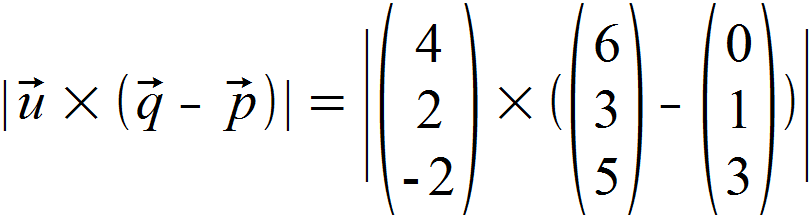
Zunächst lösen wir die Klammer auf. indem wir einfach die entsprechenden x-, y– und z-Werte der Vektoren voneinander abziehen.
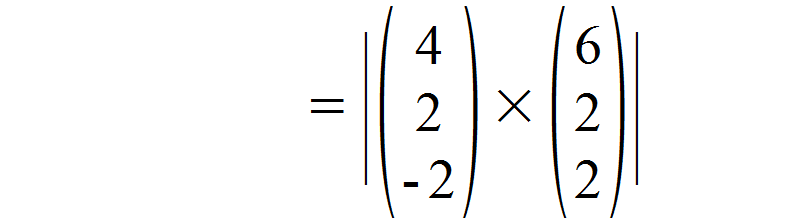
Anschließend lösen wir das Skalarprodukt nach der Regel, die wir im Hinweis weiter oben gelernt haben.
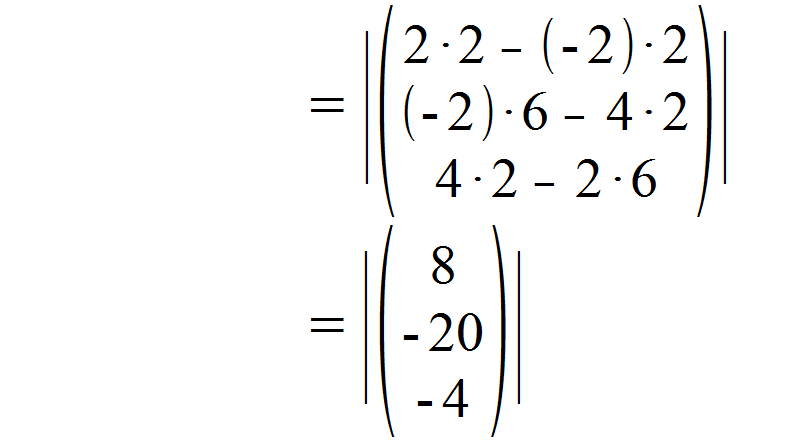
Nun liegt uns ein Vektor vor, dessen Betrag wir bestimmen können. Wir verfahren nach der zweiten Formel aus dem Hinweis und erhalten:
![]()
Lösen wir die Wurzel, erhalten wir den Wert für den Zähler unserer Formel.
![]()
Nenner
Im nächsten Schritt berechnen wir den Zähler, wofür lediglich ein Schritt notwendig ist. Wir benutzen die Formel für den Betrag eines Vektors aus den Hinweisen.
![]()
Durch Auflösen der Wurzel erhalten wir somit:
![]()
In Formel einsetzen
Im letzten Schritt setzen wir den berechneten Zähler und Nenner in unsere Formel ein.
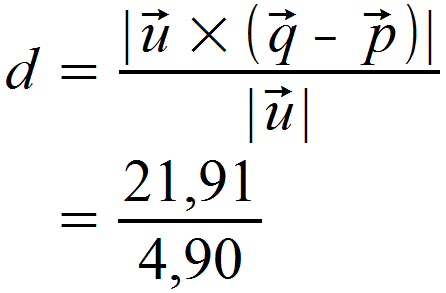
Abschließend erhalten wir also folgenden Abstand zwischen Punkt und Gerade:
![]()
