Umfang eines Dreiecks
Hier erläutern wir, wie der Umfang eines Dreiecks bestimmt wird.
Um den Umfang eines Dreiecks berechnen zu können, müssen wir wissen, was genau ein Dreieck ist.
Zur Wiederholung:
Ein Dreieck ist ein Vieleck mit drei Ecken und drei Seiten. Sowohl die Winkel als auch die Seitenlängen können sowohl alle gleich groß sein als auch alle unterschiedlich. Es gibt hier jede Variation, vgl. dazu gerne den Punkt Allgemeines Dreieck und die folgenden Seiten auf unserer Homepage.
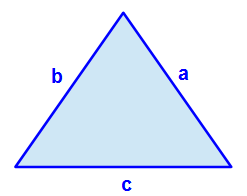
Hier sehen wir ein Allgemeines Dreieck. Die Seiten sind beschriftet mit a, b und c. Da wir bei einem Allgemeinen Dreieck davon ausgehen, dass die Seiten unterschiedlich lang sind kann man diese nicht weiter zusammenfassen.
Lerntool zu Umfang eines Dreiecks
Unser Lernvideo zu : Umfang eines Dreiecks
Die Formel des Umfangs
Bei einem Dreieck kann man nicht wie bei einem Quadrat oder Rechteck eine verkürzte Formel ermitteln. Die Berechnung des Umfangs geschieht durch Addition der einzelnen Seitenlängen:
![]()
Zu beachten gibt es immer, dass die Einheiten der Summanden gleich sind und man sie ggf. angleichen sollte. Zum Beispiel, wenn man zweimal cm und einmal mm gegeben hat.
Besonderheiten
Es gibt bestimmte Dreiecke, bei denen man die Formel des Umfangs verkürzen kann.
Das Gleichseitige Dreieck
Wie der Name sagt sind alle Seiten gleich lang.
Daraus folgt: U = 3•a
Das Gleichschenklige Dreieck
Zwei Seiten (Schenkel) dieses Dreiecks sind gleich lang.
Daher kann man den Umfang wie folgt berechnen: U = 2•a + b
Es gibt noch andere Dreiecke, diese findet ihr auch genau erläutert auf mathe-lerntipps.de. Der Umfang aller Dreiecke wird wie oben beschrieben berechnet. Desweiteren kann man unbekannte Seiten auch mit dem Satz des Pythagoras oder mit Hilfe von Winkelgrößen – Trigonometrie – berechnen. Beides findet ihr auf dieser Hompage!
Beispiel 1
Wir haben ein Dreieck und seine Seitenlängeng gegeben und möchten den Umfang des Dreiecks bestimmen.
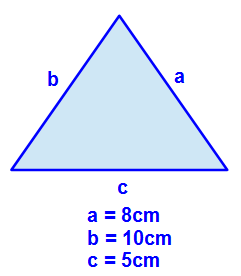
Gegeben: a = 8cm, b = 10cm und c = 5 cm
Gesucht: U
Formel: U = a + b + c
Einsetzen und berechnen: U = 8cm + 10cm + 5cm = 23cm
Antwort: Der Umfang des Dreicks ist U = 23cm.
Beispiel 2
Auch in diesem Beispiel wollen wir den Umfang des Dreiecks ermitteln. Wir müssen zunächst auf die Einheiten der Seitenlängen achten!
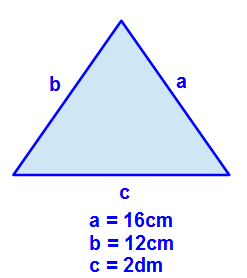
An den gegebenen Größen sehen wir, dass zwei Angaben in cm sind. Jedoch eine ist in dm. Daher müssen wir dieses zunächst angleichen! Da zwei in cm bereits vorgegeben sind, liegt es nahe die dritte Seitenlänge auch in cm umzuwandeln. 2dm = 20cm.
So haben wir nun folgende Seitenlängen: a = 16cm, b = 12 cm und c =20cm.
Nun berechnen wir den Umfang des Beispieldreiecks:
Gegeben: a = 16cm, b = 12cm und c = 20cm
Gesucht: U
Formel: U = a + b + c
Einsetzen und berechnen: U = 16cm + 12 cm + 20cm = 48cm
Antwort: Der Umfang des Dreiecks beträgt U = 48cm.
Beispiel 3
Nun betrachten wir ein Beispiel, bei dem uns nicht alle drei Seiten, sondern nur zwei Seiten und der Umfang gegeben sind:
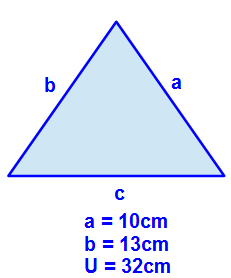
Wir sehen, es sind die Seiten a und b gegeben und zusätzlich der Umfang U. Gesucht ist hier nun die Seite c. Berechnen können wir diese, indem wir die Formel umstellen.
Gegeben;: a = 10cm, b = 13cm und U = 32cm
Gesucht: c
Umstellen der Formel nach c:
U = a + b + c | -a
U – a = b + c | -b
U – a – b = c
Nun haben wir die Formel umgestellt. Wir schreiben: c = U – a – b
Einsetzen und berechnen: c = 32cm – 10cm -13cm = 9cm
Antwort: Die Seitenlänge ist c = 9cm.
