Berechnung unbekannter Seiten
Wir zeigen hier wie man die Trigonometrie nutzen kann, um unbekannte Seiten eines Dreiecks zu berechnen.
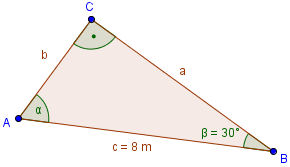
Wir haben in diesem Dreieck einen Winkel (neben dem rechten Winkel) und eine Seite gegeben. Wir müssen also noch zwei Seiten berechnen. Um die fehlenden Größen zu berechnen, benötigen wir die Trigonometrie.
Trigonometrie gehört zur Geometrie und führt uns auf das Griechische trígonon zurück, das so viel wie Dreieck bedeutet. Im Prinzip wollen wir nichts anderes machen, als die drei Größen eines Dreiecks zu berechnen:
- Seitenlänge
- Größe der Winkel
- Länge der Dreieckstransversalen
Die Funktionen der Trigonometrie, wie Kosinus, Tangens, Kotangens oder Sinus, helfen uns dabei. Wobei wir bei den Dreiecken noch kein Ende sehen. Die Experten berechnen unbekannte Größen komplexer Objekte.
Eine der Grundlagen bilden die rechtwinkligen Dreiecke, wie in der Zeichnung. Hier kommen wir auf eine Gesamtwinkelsumme von 180 Grad. Der rechte Winkel ist zugleich der größte der drei Innenwinkel.
- Die Hypotenuse liegt gegenüber vom rechten Winkel und ist die längste Seite des rechten Winkels.
- Katheten – das sind die beiden kürzeren Seiten unseres Dreiecks.
- Gegenkathete – der Winkel gegenüber.
- Ankathete – der Nachbar des gegebenen Winkels.
Dabei spielt es eigentlich keine Rolle, wenn Dreiecke zum Beispiel viel längere Seiten haben: Die Brüche bleiben gleich. Kennt ihr also die Funktion der einzelnen Winkel, seid ihr einen beträchtlichen Schritt weiter.
Lerntool zu Berechnung unbekannter Seiten
Unser Lernvideo zu : Berechnung unbekannter Seiten
Berechnung von b
Wir beginnen mit der Seite b. Wir benötigen also eine Formel um b zu berechnen. In dieser Formel darf nur b als Unbekannte enthalten sein. Wir haben jetzt die Auswahl zwischen Sinus, Kosinus und Tangens. Da b die Gegenkathete von β darstellt kommt nur Sinus und Tangens in Frage, da Kosinus nur mit der Ankathete arbeitet. Bei Tangens ist das Problem, dass Tangens neben der Gegenkathete auch die Ankathete a benötigt und wir diesen noch nicht kennen. Wir müssen also Sinus benutzen, da Sinus mit der Hypotenuse arbeitet und wir die Hypotenuse c bereits kennen. Wir stellen also folgende Formel auf:
![]()
Wir setzen die bekannten Größen ein und lösen die Gleichung nach b auf:
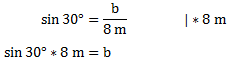
Diesen Term können wir nun in den Taschenrechner eingeben und erhalten als Ergebnis:
![]()
Die Seite b ist 4 m lang.
Berechnung von a (Trigonometrie)
Als nächstes berechnen wir die Seite a. Genau wie eben haben wir wieder die Wahl zwischen Sinus, Kosinus und Tangens vom Winkel β. Kosinus und Tangens benutzen beide die fehlende Ankathete a. Da wir die beiden anderen Seiten ebenfalls kennen, können wir uns zwischen Kosinus und Tangens entscheiden. Für Kosinus brauchen wir die Seiten a und c und für Tangens die Seiten a und b. Es ist nun etwas besser den Kosinus zu benutzen, da wir hier die gegebene Seite c benötigen. Bei Tangens benötigen wir die eben berechnete Seite b. Wenn wir Tangens benutzen gehen wir das Risiko eines Folgefehlers ein, falls wir bei der Berechnung von b einen Fehler gemacht haben sollten. Es ist deshalb immer besser, wenn möglich die Werte zu benutzen die gegeben sind und dadurch auf jeden Fall stimmen. Natürlich hat man diese Wahl aber nicht immer. Wir benutzen folgende Formel:
![]()
Genau wie bei der Rechnung für b setzen wir die bekannten Größen ein und formen die Gleichung nach a um.
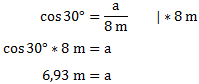
Als Ergebnis erhalten wir a = 6,93 m.
Berechnung von a (Pythagoras)
Wenn wir zwei Seiten eines rechtwinkligen Dreiecks kennen und die dritte Seite berechnen wollen, können wir natürlich nach wie vor den Pythagoras nutzen. Der Pythagoras lautet:
![]()
c ist dabei immer die Hypotenuse. Da in unserem Dreieck c ebenfalls die Hypotenuse ist, stimmen die Bezeichnungen überein. Wir müssen die Formel also nun nach a umstellen:
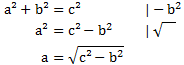
Nun können wir die Werte von c und b einsetzen:
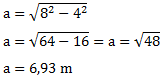
Natürlich erhalten wir auf diesem Weg dasselbe Ergebnis. In diesem Beispiel ist es egal welchen Weg man geht. Es gibt jedoch Situationen in denen man Aufgrund der gegebenen Werte nur einen von beiden gehen kann.
