Einführung in die Prozentrechnung
Im Leben begegnen uns sehr oft Prozentangaben. Daher ist es wichtig damit umgehen zu können. In Kaufhäusern sind Rabatte zum Beispiel oft in Prozent angegeben. Wie berechnen wir aber, wie viel ein Artikel nun tatsächlich kostet und wie viel wir eigentlich sparen?
Hierfür müssen wir uns zunächst ein paar grundsätzliche Sachen klarmachen.
Unser Lernvideo zu : Einführung in die Prozentrechnung
Was bedeutet überhaupt Prozent?
„Prozent“ bedeutet erst einmal nichts anderes als Hundertstel. 1 Prozent bedeutet also im Prinzip 1 Hundertstel also 0,01. Genauso kann man Prozentangaben auch schreiben. Man kann also jeden Bruch und jede Dezimalzahl in einen Prozentwert umrechnen.
Umgekehrt kann man natürlich auch jede Prozentzahl in eine Dezimalzahl oder Bruch umrechnen. Um von einer Prozentzahl zu der dezimalen Schreibweise zu gelangen, muss man den Wert also lediglich durch 100 teilen.
Beispiele
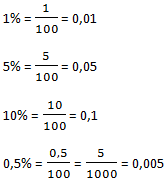
Aber was sagt uns nun ein Wert von 1%? Es handelt sich dabei wie eben schon gesagt um 1 Hundertstel. Und zwar ein Hundertstel vom Grundwert. Wenn wir also 1% von 100€ berechnen wollen, ist damit ein Hundertstel von 100€ gemeint. Also 1€.
Ähnlich wie bei der Bruchrechnung hier ein paar Beispiele für einige Prozentsätze:
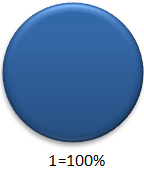
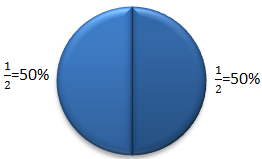
100% bedeutet ein Ganzes. 50% ist genau die Hälfte.
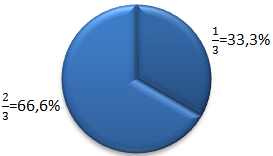
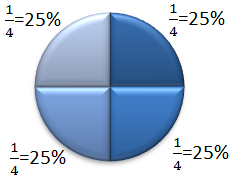
Links sehen wir 33,3% und 66,6%. Rechts 25%.
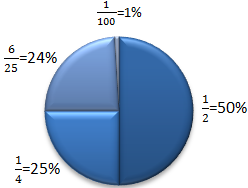
Hier noch ein etwas komplexeres Beispiel mit mehreren verschiedenen Prozentsätzen. Ein ganzer Kreis ist dabei immer 100%. Wenn man also alle Prozentangaben in die der Kreis eingeteilt ist addiert, muss immer 100% rauskommen.
Wozu brauchen wir Prozente?
Prozente braucht man immer dann, wenn man keine absoluten Angaben machen möchte. Wenn man zum Beispiel sagt in Milch sind 3,5% Fett, ist damit noch nicht klar wie viel Gramm Fett in der Milch tatächlich sind.
Der absolute Fettgehalt ist natürlich abhängig von der Menge. Kauft man eine große Packung Mild ist die absolute Fettmenge natürlich größer als wenn man eine kleine Packung Milch kauft. Die Prozentzahl ermöglichen es uns also den Fettanteil unabhängig von der tatsächlichen Menge anzugeben.
Ähnlich ist es bei Rabattaktionen. Wenn ein Kaufhaus 10% Rabatt auf alle Artikel gibt, ist noch nicht klar, wie viel Euro man bei einem Einkauf sparen wird.
Dies wird erst klar, wenn man sich für einen Artikel entschieden hat. Wenn wir uns für einen 100€ teuren Artikel entscheiden sparen wir 10% von 100€, also 10€. Wenn wir uns für einen 5€ teuren Artikel entscheiden, sparen wir nur 10% von 5€, also 0,50€.
Oft ist es auch einfach deutlich verständlicher Prozentangaben statt absolute Angaben zu machen. Wenn wir zum Beispiel sagen, dass 51% der Einwohner Deutschlands weiblich sind ist dies sicherlich leichter und schneller zu verstehen als wenn wir sagen, dass 41,718 Millionen von 81,8 Millionen Menschen in Deutschland weiblich sind.
Außerdem ist die Vergleichbarkeit mit anderen Ländern sehr viel einfacher wenn man Prozentsätze benutzt als wenn man absolute Werte angibt. Andersrum gibt es natürlich auch Situationen in denen man tatsächlich die absoluten Werte benötigt. Man muss also von Fall zu Fall entscheiden welche Angabe sinnvoller ist.
Wichtige Begriffe
- Grundwert: Dies ist der Wert auf den sich die Prozentangaben beziehen. Der Grundwert entspricht 100%.
- Prozentsatz: Dies ist die Prozentzahl. Beispielsweise 5%, 10%… Sie bezieht sich auf den Grundwert.
- Prozentwert: Der Wert dem der Prozentsatz entspricht. Er hat die gleiche Einheit wie der Grundwert.
Beispiel: 10% von 50€ sind 5€
Bei diesem Beispiel ist unser Grundwert 50€. Auf diesen Wert bezieht sich die Prozentangabe. 50€ ist also das Ganze beziehungsweise 100%. 5€ ist der Prozentwert. 5€ sind also 10% von 50€. Zu guter Letzt bleiben noch die 10%, die man Prozentsatz nennt.
Allgemeine Formel
Die allgemeine Formel für die Prozentaufgaben ist:
![]()
Wir müssen also den Prozentwert durch den Grundwert teilen um den Prozentsatz zu erhalten. Es gibt nun drei verschiedenen Situationen mit denen wir umgehen können müssen. Diese sind:
- Berechnung des Prozentwerts wenn Grundwert und Prozentsatz gegeben sind.
- Berechnung des Grundwerts wenn Prozentwert und Prozentsatz gegeben sind.
- Berechnung des Prozentsatzes wenn Prozentwert und Grundwert gegeben sind.
Diese drei Aufgabentypen behandeln wir in den folgenden Artikeln.
