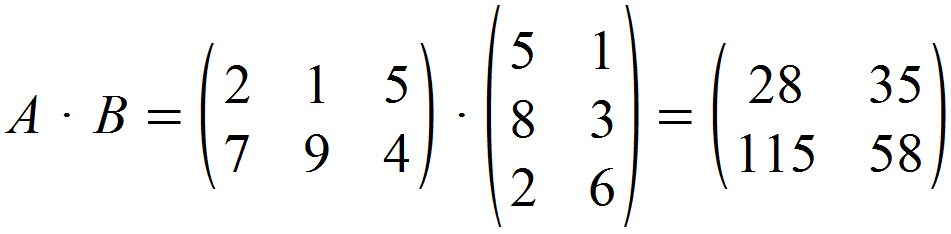Multiplikation von Matrizen
Auch Matrizen können miteinander multipliziert werden, wodurch als Produkt eine neue Matrix entsteht. Die Elemente des Produkts werden bestimmt, indem das Skalarprodukt aus dem Zeilenvektor der ersten Matrix und dem Spaltenvektor der zweiten Matrix gebildet wird. Hierfür muss die Spaltenanzahl der ersten Matrix mit der Zeilenanzahl der zweiten Matrix übereinstimmen. Das Produkt zweier Matrizen wird auch Matrixprodukt genannt.
Beispiel
Gesucht ist das Produkt der Matrizen A und B, die wie folgt definiert sind:
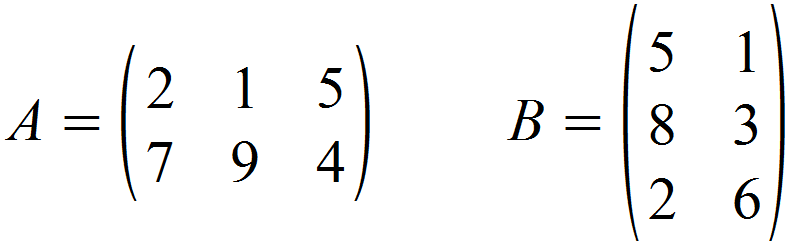
![]()
Die erste Matrix A ist eine (2,3-)-Matrix, die zweite Matrix B eine (3,2)-Matrix. Demnach verfügt die Matrix A um drei Spalten und die Matrix B über drei Zeilen, weshalb unsere Bedingung erfüllt ist und sie miteinander multiplizierbar sind. Aber wie verfährt man jetzt?
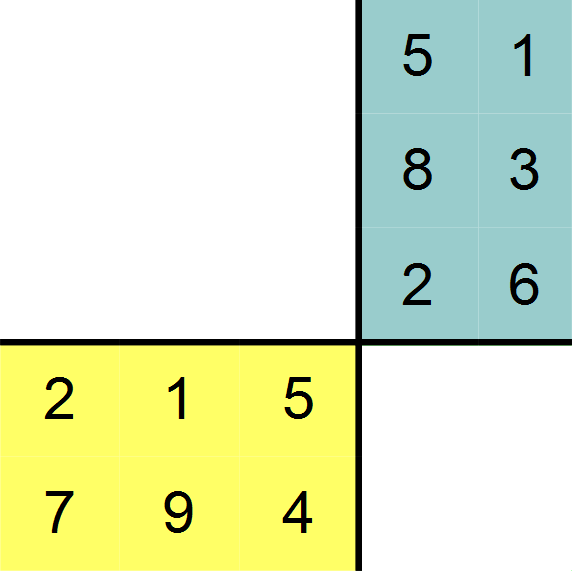
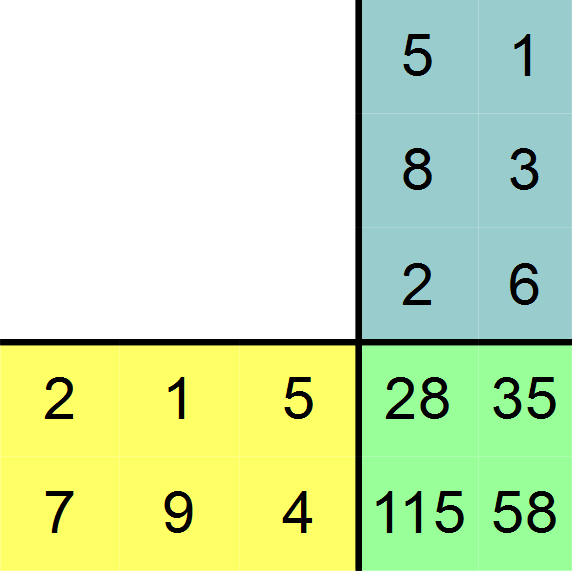
Man geht am besten nach dem Falk-Schema vor, welches hier beispielhaft an den Matrizen A und B gezeigt werden soll. Wir zeichnen ein Kreuz und tragen die Matrix A unten links ein, hier in gelb markiert. Matrix B wird oben rechts eingetragen, hier in blau unterlegt.
Das Matrixprodukt wird nun unten rechts eingetragen. Wir setzen zunächst die Variablen a, b, c und d für die Elemente des Matrixprodukts ein, um auf deren exakte Werte im weiteren Verlauf genauer einzugehen.
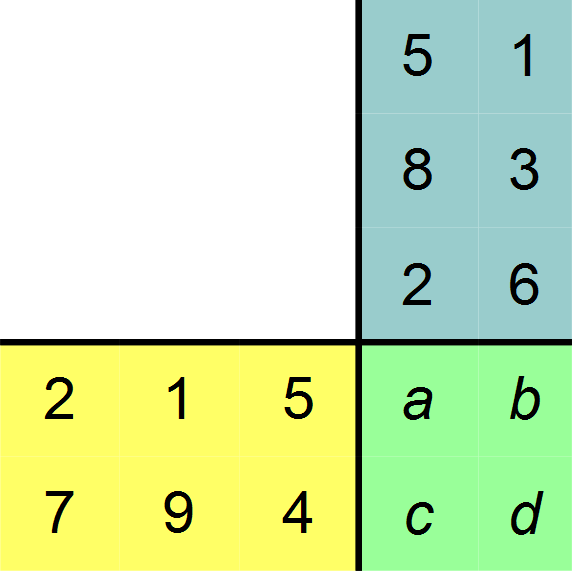
Gesucht ist also eine (2,2)-Matrix, die hier grün dargestellt ist. Für dessen Elemente müssen wir das Skalarprodukt der jeweiligen Zeile der Matrix A und der jeweiligen Spalte der Matrix B bestimmen. Für das Element a sieht das folgendermaßen aus:
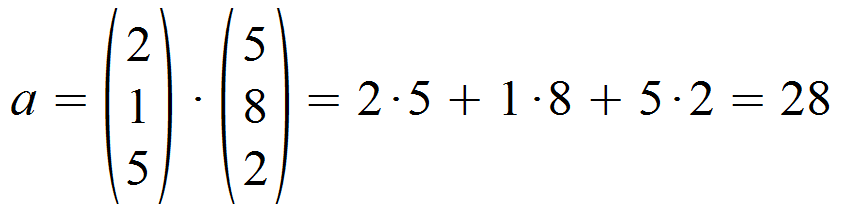
Die Berechnung der anderen Elemente b, c und d erfolgt auf identische Weise.
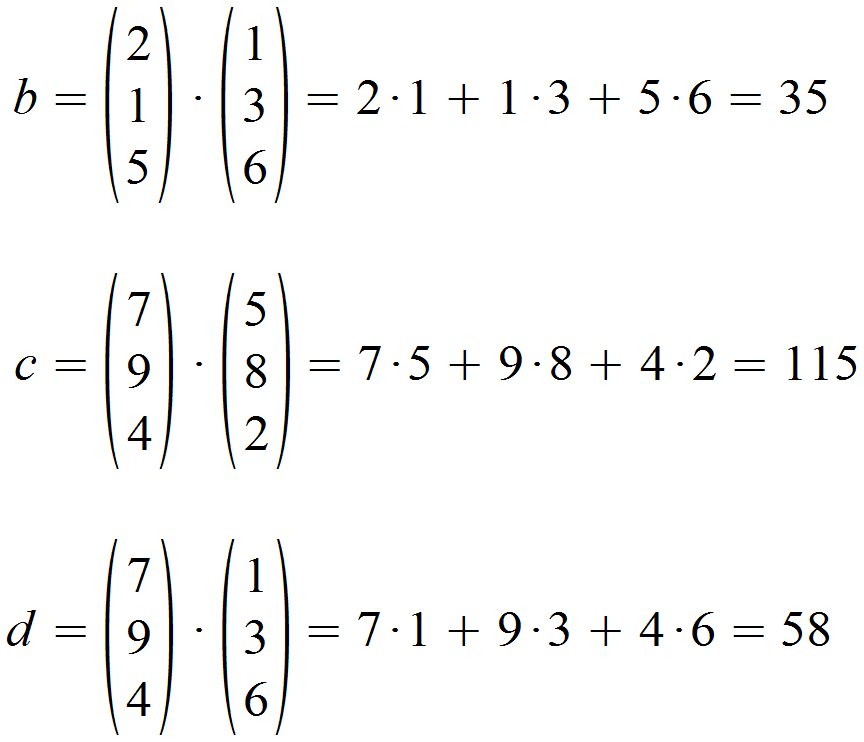
Wir erhalten für unser Falk-Schema also folgende Zahlenwerte:
Demnach ergibt die Multiplikation der Matrizen A und B folgendes Matrixprodukt: