Bestimmen der Funktionsvorschrift aus zwei Punkten
Wie man mit nur zwei gegebenen Pukten die Funktionsvorschrift einer linearen Funktion bestimmt erklären wir hier.
Mit zwei gegebenen Pukten die Funktionsvorschrift einer linearen Funktion bestimmen
Alles was benötigt wird um die Funktionsvorschrift einer linearen Funktion zu bestimmen, haben wir in den vorhergehenden Artikeln bereits erläutert. Lediglich die rechnerische Methode zur Bestimmung des y-Achsenabschnitts ist neu.
Gegeben sind die Punkte:
![]()
Wir zeichnen die beiden Punkte in ein Koordinatensystem ein. Dies dient dem besseren Verständnis und muss nicht unbedingt getan werden.
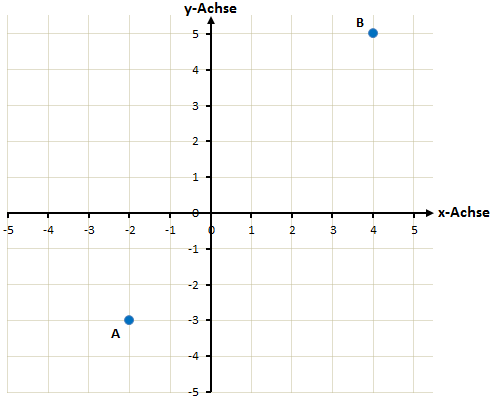
Diese beiden Punkte sollen also mit einer linearen Funktion miteinander verbunden werden.
Wir bestimmen nun zunächst die Steigung a. Dazu zeichnen ein Steigungsdreieck und bestimmen Δx und Δy.
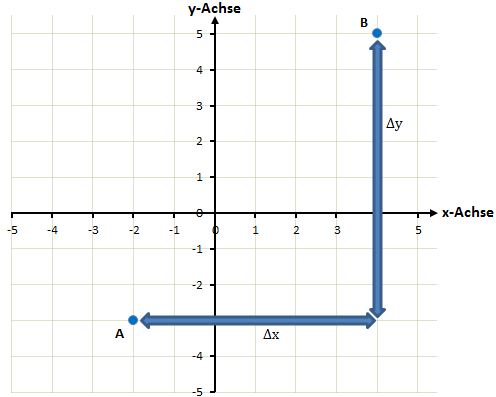
Für Δy subtrahieren wir die beiden y-Koordinaten:
![]()
Für Δy subtrahieren wir die x-Koordinaten:
![]()
Jetzt teilen wir Δy durch Δx und erhalten die Steigung a:
![]()
Jetzt fehlt uns nur noch der y-Achsenabschnitt. Diesen können wir grafisch bestimmen indem wir die Beiden Punkte miteinander verbinden und den Schnittpunkt mit der y-Achse ablesen oder rechnerisch indem wir eine der folgenden Formeln anwenden:
![]()
Wir setzen die Werte in die erste Formel ein:
![]()
Natürlich hätten wir auch die zweite Formel nehmen können:
![]()
In beiden Fällen bekommen wir natürlich dasselbe Ergebnis.
Die Funktionsvorschrift lautet damit:
![]()
Welche der beiden Schreibweisen man wählt ist Geschmackssache. Die mathematische Bedeutung ist in beiden Fällen identisch.
Alternatives Vorgehen: y-Achsenabschnitt b grafisch ablesen
Wir hätten den y-Achsenabschnitt auch grafisch ablesen können. Dabei wäre das Ergebnis aber nicht ganz so genau, wie bei dem rechnerischen Vorgehen. Um den y-Achsenabschnitt ablesen zu können müssen wir zunächst die beiden Punkte A und B verbinden.
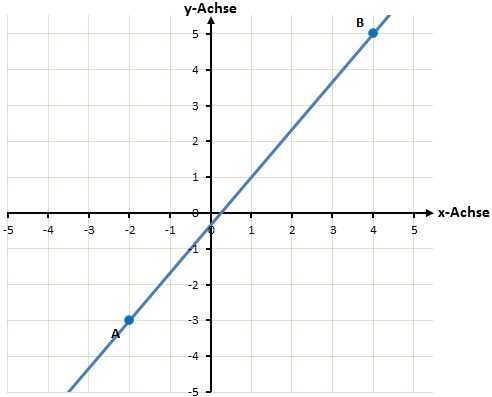
Jetzt können wir den Schnittpunkt mit der y-Achse ablesen. Allerdings ist dies schwierig. Wir müssen den Schnittpunkt ungefähr Schätzen. Vermutlich würden wir noch sehen, dass der Schnittpunkt etwas über -0,5 liegt. Vielleicht würden wir also -0,4 schätzen.
Dies ist nicht weit weg vom genauen Wert, dennoch merken wir, dass diese Methode nur benutzt werden kann, wenn wir den Wert nicht exakt benötigen. Die Methode ist dennoch gut um das rechnerische Ergebnis zu überprüfen.
