Schriftliches Multiplizieren
1. Faktor · 2. Faktor = Produkt
Rechner Schriftliches Multiplizieren
Unser Lernvideo zu : Schriftliches Multiplizieren
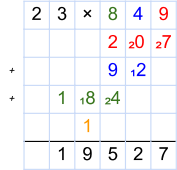
Beispiel: 23 · 849 (Mal rechnen)
Um diese beiden Zahlen zu multiplizieren, schreibt man sie zunächst nebeneinander in eine Tabelle und trennt sie durch ein Malzeichen. Für jede Stelle des 2. Faktors lassen wir eine Zeile plus eine Übertragszeile frei. In diesem Fall vier freie Zeilen und dann ein Trennstrich.
Wir nehmen uns nun die rechte Zahl (hier 849) Stelle für Stelle vor. Beim Rechnen bewegen wir uns dabei von rechts nach links.
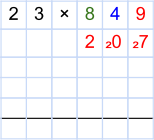
Beginnen wir also mit der rot eingefärbten 9. Diese multiplizieren wir mit dem 1. Faktor (der 23). Auch hierbei gehen wir von rechts nach links vor. Wir multiplizieren also als erstes die 9 mit der 3 (9 · 3 = 27) und tragen das Ergebnis direkt unter der 9 ein. Die Einerstelle (die 7) wird dabei groß in das Feld eingetragen und die zweite Stelle (die 2) als Übertrag klein daneben als Merkhilfe. Vielen ist dies als „2 im Sinn“ geläufig.
Dann multiplizieren wir die 9 mit der nächsten Stelle (der 2 vom ersten Faktor). Das Ergebnis ist 18 (9 · 2 = 18). Dies addieren wir mit dem Übertrag 2, 18 + 2 = 20. Wir schreiben also eine große 0 in das Feld neben der großen 7 und notieren wieder eine kleine 2 als Übertrag im selben Feld.
Nun würden wir uns die nächste Stelle des ersten 1. Faktors vornehmen. Da dieser aber nur zwei Stellen hat, sind wir hier vorerst fertig. Als einziges ist noch die 2 aus dem Übertrag in das Feld daneben zu notieren, damit auch dieser später berücksichtigt wird. Wir schreiben also links neben die 0 eine große 2.
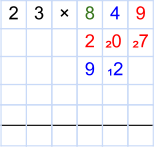
Wir nehmen nun die nächste Stelle des 2. Faktors (die blaue 4). Mit dieser gehen wir genauso vor wie eben mit der 9. Wir multiplizieren sie also Stelle für Stelle mit dem ersten Faktor. Auch hier arbeiten wir uns wieder von rechts nach links vor und multiplizieren die 4 mit der 3 (letzte Stelle des 1. Faktors). Das Ergebnis (4 · 3 = 12) notieren wir in der nächsten freien Zeile unter der blauen 4. Dabei schreiben wir wieder die 2 groß und die 1 als Übertrag klein daneben.
Im nächsten Schritt ist die 4 mit der 2 zu multiplizieren (4 · 2 = 8). Wir addieren den Übertrag von der vorhergehenden Rechnung (8 + 1 = 9) und tragen links neben der großen 2 eine große 9 ein. In diesem Fall gibt es keinen Übertrag und die 9 bleibt alleine im Feld stehen.
Die letzte Stelle des 2. Faktors ist die grüne 8. Das Prinzip bleibt gleich und wir multiplizieren zunächst 8 mit 3 (8 · 3 = 24). Das Ergebnis tragen wir unter der grünen 8 in der nächsten freien Zeile ein. Wir notieren hier also eine große 4 und eine kleine 2 als Übertrag. Die nächste Rechnung ist 8 · 2 = 16. Dazu müssen wir noch den Übertrag der letzten Rechnung addieren (16 + 2 = 18). Wir schreiben also eine große 8 auf und eine kleine 1. Da wir hier wieder am Ende der Rechnung sind, tragen wir die 1 außerdem noch in das Kästchen links daneben ein.
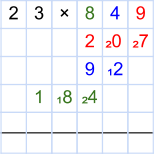
Wir haben nun alle Zahlen multipliziert und kommen zum nächsten Schritt. Hierfür führen wir eine schriftliche Addition durch. Die erste Zeile (23 · 849) wird dabei natürlich nicht beachtet. Wir gehen dabei so vor, wie es in dem Kapitel der schriftlichen Addition erklärt wurde. Dabei beachten wir nur die groß geschriebenen Zahlen und vernachlässigen die kleinen, da diese ja bereits berücksichtigt wurden. In allen Feldern, in denen keine Zahl steht, denken wir uns eine 0. Wir kommen auf das Ergebnis 19527, welches das Endergebnis unser Multiplikation ist (23 · 849 = 19527).
Negative Zahlen
Es gilt: Multipliziert man zwei Zahlen mit dem gleichen Vorzeichen, so ist das Ergebnis immer positiv. Multipliziert man zwei Zahlen mit unterschiedlichen Vorzeichen (eine positive und eine negative Zahl), so ist das Ergebnis immer negativ. Bei der Rechnung kann man das Vorzeichen einfach weglassen. Erst beim Ergebnis schreibt man ein Plus (dieses kann man auch weglassen) oder ein Minus vor die Zahl.
Normalerweise schreibt man mehrere Rechenzeichen nicht einfach hintereinander. Wenn man zum Beispiel 3 mit -4 multiplizieren möchte, schreibt man die -4 in Klammern, da sonst das Mal- und das Minuszeichen direkt hintereinander stehen würden. Als Hinweis dafür, dass das Minus kein Operator sondern lediglich das Vorzeichen der 4 ist, schreibt man die -4 in Klammern.
Beispiele:
3 · (-4) = -12
-3 · 4 = -12
-3 · (-4) = 12
3 · 4 = 12
Weitere wichtige Rechenregeln der Multiplikation
Eine Zahl mit 1 multipliziert ergibt die Zahl selbst.
Beispiel: 345 · 1 = 345
Eine Zahl mit 0 multipliziert ergibt immer 0.
Beispiel: 345 · 0 = 0
Man kann die Reihenfolge der Faktoren vertauschen und erhält trotzdem immer das selbe Ergebnis (Kommutativgesetz).
Beispiel: 3 · 4 = 4 · 3
Kopfrechnen und Eselsbrücken
Es gibt Methoden, mit denen man auch größere Zahlen einfach im Kopf rechnen kann. Natürlich existieren hierbei Grenzen. Besonders das Gedächtnis wird bei dieser Methode gefordert, da man sich die Zwischenergebnisse merken muss, während man den nächsten Teil der Aufgabe löst. Außerdem ist das sichere Addieren im Kopf vorauszusetzen.
Zahlen mit Nullen am Ende
Wenn man Zahlen multiplizieren möchte, an deren Ende eine oder mehrere Nullen stehen, so kann man den Rechenvorgang vereinfachen. Während der Rechnung kann man alle Nullen am Ende einer Zahl zunächst streichen. Man muss nur daran denken, am Ende genau die gleiche Anzahl an Nullen dem Ergebnis wieder hinzuzufügen.
Beispiel: anstatt 40 · 3 rechnen wir 4 · 3 = 12 und fügen dem Ergebnis eine Null hinzu. 40 · 3 = 120.
Beispiel: statt 300 · 2100 rechnen wir 3 · 21 = 63 und fügen dem Ergebnis wieder 4 Nullen hinzu, die wir vorher gestrichen hatten. 300 · 2100 = 630000.
Zahlen schrittweise multiplizieren
Um etwas größere Zahlen im Kopf zu multiplizieren, kann man sie zunächst sinnvoll in kleinere Zahlen zerlegen.
Wir rechnen also nicht 54 · 27, sondern zerlegen die 54 in 50 + 4 und die 27 in 20 + 7. Wir erhalten dann (50 + 4) · (20 + 7). Anschließend multiplizieren wir diesen Ausdruck nach dem Distributivgesetz aus. Der Vorteil dieses Verfahrens ist, dass man mit Hilfe der vorherigen Regel („Zahlen mit Nullen am Ende“) nur noch relativ kleine Zahlen multiplizieren muss und diese dann im letzten Schritt addiert.
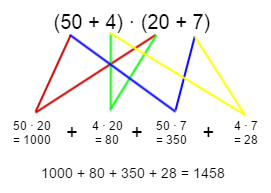
Wir rechnen so systematisch alle Ergebnisse aus und addieren diese anschließend. Das Ergebnis der Multiplikation ist also 1458.
Einsteiger Übungsaufgaben – schriftliches Multiplizieren
6 2 • 1 4 1 8 • 1 6 3 9 • 2 4 3 5 • 2 8
4 5 • 2 2 2 7 • 3 3 6 9 • 1 2 4 6 • 1 9
Profi Übungsaufgaben – schriftliches Multiplizieren
8 6 3 2 • 976 7 4 9 • 8 4 9 3 6 2 • 7 4 3 4 2 7 5 • 7 7 2
6 6 4 3 • 4 3 2 0 4 5 • 2 3 3 6 9 9 • 7 7 1 2 0 0 • 8 4 3 2
Wie du schon bald ohne Probleme schriftlich Multiplizieren kannst?
Achtet darauf, die Zahlen ordentlich nebeneinander und untereinander zu schreiben. Denn nur so behaltet ihr selbst bei schwierigen Aufgaben den Überblick. Ihr müsst noch nicht mal zu den Mathecracks gehören, um diese Aufgaben ordentlich zu lösen. Mit der oberen Methodik könnt ihr garantiert alle Aufgabentypen im Bereich schriftliches Multiplizieren korrekt ausrechnen.
Die Basis legt die Multiplikation und das 1×1 aus der Grundschule, das noch auswendig gelernt werden muss. Wenn du jeden Tag nur ein paar dieser Übungsaufgaben löst, dann wirst du schon bald keine Probleme mehr mit diesen Rechenverfahren haben.
Hinweis: Wir nutzen das schriftliche Multiplizieren nur für komplexe Aufgabe sowie mehrstellige Zahlen. Die einfachen Rechnungen erledigst du nach wie vor im Kopf.
Eigentlich setzt sich selbst eine komplexe Aufgabe aus vielen einzelnen Multiplikationen zusammen, die wir bereits in der Grundschule gelernt haben. Im Anschluss folgt die schriftliche Addition und schon haben wir das richtige Ergebnis.
Probe: Um herauszufinden, ob dein Ergebnis richtig ist, multipliziere die Zahlen einfach in umgekehrter Richtung miteinander – kommt dasselbe Ergebnis heraus, bist auf einem guten Weg.
