Assoziativgesetz
Dieses Gesetz erlaubt uns unterschiedliche Teile in einer Rechnung zu verbinden. Durch geschicktes Verbinden von Teilen können wir uns so einen Rechenvorteil verschaffen. Wir können dieses Gesetz aber auch dafür benutzen, um Klammern aufzulösen.
Die allgemeine Schreibweise sieht so aus:
Addition
(a + b) + c = a + (b + c)
Multiplikation
(a • b) • c = a • (b • c)
Unser Lernvideo zu : Assoziativgesetz
Addition
Wir können uns also aussuchen, ob wir zuerst a + b rechnen und dann c addieren oder erst b + c und dann a addieren. Wir können die Klammern natürlich auch komplett weglassen und schreiben:
(a + b) + c = a + (b + c) = a + b + c
Beispiel
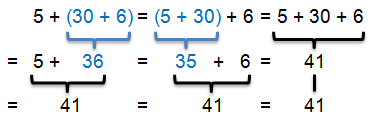
Rechenvorteile
Insbesondere in Zusammenhang mit dem Kommutativgesetz kann man sich durch dieses Gesetz oft Vorteile bei der Rechnung verschaffen.
Beispiel
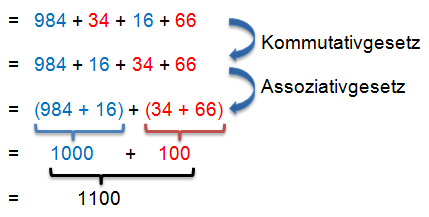
Durch geschicktes Vertauschen und das Setzen von Klammern konnten wir hier erreichen, dass die Addition der einzelnen Teile sehr leicht wird und wir dadurch bei der Rechnung Zeit sparen.
Multiplikation
Genau wie bei der Addition können auch bei der Multiplikation beliebig Klammern gesetzt oder weglassen werden. Da auch die Multiplikation kommutativ ist, können wir uns so viele Rechnungen vereinfachen.
Beispiel
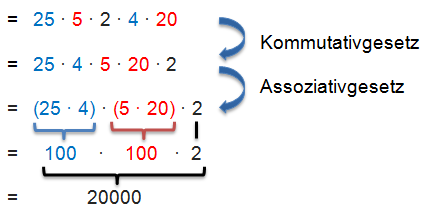
Interessante Fragen und Antworten zu Assoziativgesetz
Was ist ein Neutrales und ein Inverses Element ist in der Algebra? |
Das neutrale ElementEin neutrales Element in der Mathematik zeichnet sich dadurch aus, dass es weder den vorangegangenen, noch den nachfolgenden Wert verändert. Beispiel: x+0=x oder auch 0+x=x Die Zahl 0 kann zu einem beliebigen Element x addiert werden, ohne dass sich das Element x verändert. Deshalb wird die Zahl 0 auch als das neutrale Element der Addition bezeichnet. Auch in der Multiplikation gibt es ein neutrales Element. Beispiel: x*1=x oder auch 1*x=x Auch hier kann die Zahl 1 mit einem beliebigen Element x multipliziert werden, ohne dass sich das Element x verändert. Deshalb gilt die Zahl 1 als das neutrale Element der Multiplikation. Das inverse ElementVerknüpft man eine beliebige Zahl mit seinem inversen Element, dann ergibt dies immer das neutrale Element. Beispiel: 4+(-4)=0 Als Ergebnis steht das neutrale Element der Addition. Die Zahl -4 ist in diesem Fall dann das inverse Element zur Zahl 4. Um das inverse Element einer beliebigen Zahl in der Multiplikation zu bilden, muss das Reziproke (Kehrwert) dieser Zahl gebildet werden. Beispiel: 4*1/4=1 In diesem Fall ist 1/4 das inverse Element der Zahl 4 in Hinsicht auf die Multiplikation. |
