Fläche zwischen Funktionen
Integrale berechnen den gewichteten Flächeninhalt, das heißt Beiträge unterhalb der x-Achse zählen negativ.
Vorgehensweise
•Schnittpunkte berechnen
•f(x)−g(x) berechnen
•Integrieren
► Damti F eine Stammfunktion zu f ist, muss gelten: F`(x) =f(x)
Man schreibt: ∫f(x)dx=F(x)+C
wobei C eine beliebige Konstante ist, da es zu jeder Funktion beliebig viele Stammfunktionen gibt, die sich nur in der Konstante unterscheiden (die fällt ja beim Ableiten wieder weg)
Beispiele:
Ist F mit F(x)=x3+x2 eine Stammfunktion zu f mit f(x)=3x2+2x ?
Da F′(x)=3x2+2x= f(x), ist F Stammfunktion zu f.
Das unbestimmte Integral von f(x)=3x2+2x ist ∫f(x)dx=x3+x2+C
Unser Lernvideo zu : Fläche zwischen Funktionen
Rechenbeispiel
Wir wollen den Flächeninhalt der Fläche zwischen den Funktionen
f(x)= x+3 und g(x)= x2+1
Zuerst bestimmen wir die Grenzen
Schritt 1: Schnittstellen berechnen
Wir setzen beide Funktionen gleich und lösen nach x auf. Nullstellen also!
→ f(x)= g(x)
→ x+3 = x2+1
→ 0 = x2-x-2
Mit der pq Formel können wir nun lösen.
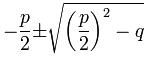
x2-x-2= 0
x1= 0,5 – √2,25 → x1 = -1
x2=0
Schritt 2: einzelne Integrale bilden
→ ∫ f(x) -g(x) dx
→ [ -1/3x 3 +1/2x2 +2x] → Integral geht von 2 bis -1. Also beim Integralzeichen oben eine 2 und unten eine -1
= 1/3*8 + 1/2 *4 +4 – ( 1/3 +1/2 -2)
= -3 +8 -0,5
=4,5 FE
Der Flächeninhalt zwischen den Funktionen beträgt 4,5 FE ( Flächeneinheiten)
