Kongruent
Zwei oder mehr Dreiecke sind kongruent, das bedeutet deckungsgleich, wenn man diese durch spiegeln, drehen oder verschieben auf einander legen kann.
Unser Lernvideo zu : Kongruent
Beispiel: Kongruent
Wir haben zwei Dreiecke:
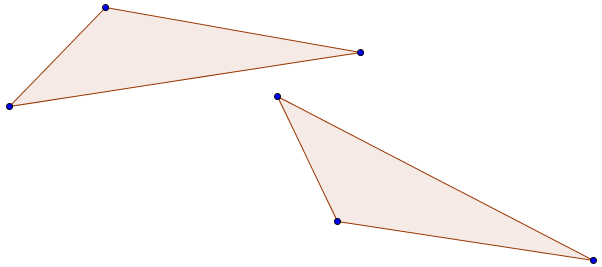
Sind diese Kongruent?
Ja! Denn wir haben das eine Dreieck durch eine Achsen- und Punktspiegelung des anderen erzeugt.
Zunächst eine Achsenspiegelung:
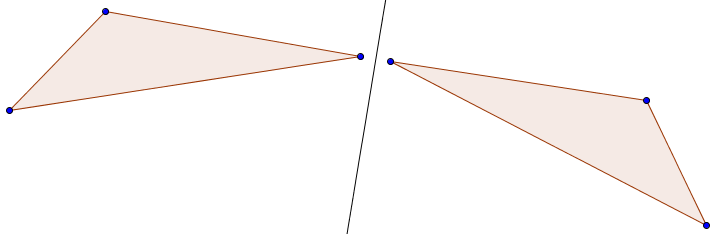
Und anschließend noch eine Punktspiegelung:
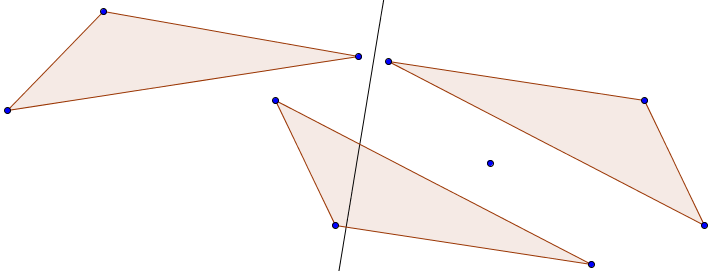
Alle drei gezeigten Dreiecke sind also kongruent.
Kongruent – deckungsgleiche Formen
Den Begriff „Kongruent“ verwenden Mathematiker im Zusammenhang mit zwei oder mehreren Dreiecken. Dreiecke sind kongruent, was bedeutet, dass diese deckungsgleich sind. Deckungsgleich meint, dass durch das Spiegeln, Verschieben oder Drehen eines Dreieckes, es direkt auf das zweite passt. Die einfachste Methode ist es, das Dreieck auf ein Blatt Papier zu zeichnen, auszuschneiden und zu prüfen, ob es mit allen Seiten und Winkeln mit dem anderen gleich ist. Für das Herausfinden ob, eine Kongruenz besteht, existieren einige Merksätze und Tipps.
In der Geometrie kommen zahlreiche andere Figuren vor, die mithilfe einer Kongruenzabbildung übereinander gleich sind. Die Kongruenzabbildung ist eine Bewegung, die durch eine Drehung, Parallelverschiebung, Spiegelung oder durch Verknüpfen dieselbe Form ergibt.
Kongruenzabbildungen
Unter dem Begriff der Kongruenzabbildung ist ein Bewegungsvorgang einer Figur zu verstehen, nach dem sich die Form und die Größe nicht verändern. Die Kongruenzabbildung entspricht nach jeder Bewegung immer der ursprünglichen Figur. Aus diesem Grund existieren vier Arten der Kongruenzabbildung:
- Drehung
- Achsenspiegelung
- Punktspiegelung
- Parallelverschiebung
In den einfachsten Fällen reicht eine Bewegungsart aus, um zu erkennen, ob es sich um kongruente Formen handelt. Allerdings existieren Knifflige, bei denen es sich anbietet, mehrere Kongruenzabbildungen vorzunehmen. Welche Art der Abbildung die richtige ist, hängt individuell vom Anwender und der vorliegenden Situation ab. Meist gibt die Position und Ausrichtung der Formen an, wie weiter vorzugehen ist. Ist einzig eine Parallelverschiebung notwendig, ist es nahezu auf den ersten Blick zu erkennen, dass die Figuren kongruent sind. Bei einer Spiegelung oder Drehung benötigt der Mathematiker ein geübtes Auge.
Ähnliche und Deckungsgleiche Formen
Um diesen Begriff besser zu veranschaulichen, folgt ein kleines Beispiel:
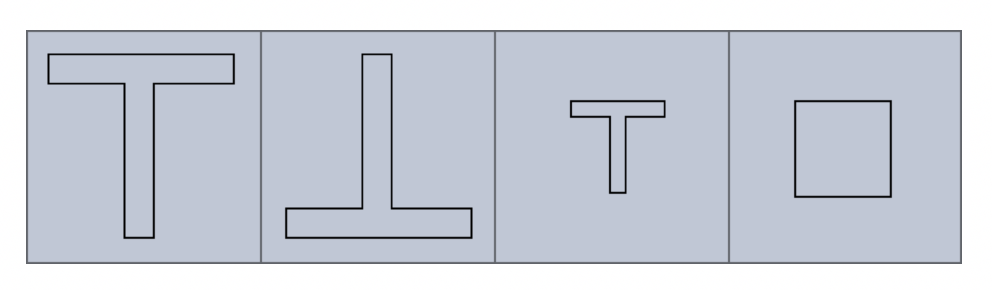
Bei dieser Abbildung sind die ersten beiden Figuren kongruent. Das Einzige was sie unterscheidet, ist ihre Lage. Dreht der Anwender die zweite Form um 180 Grad, erhält er dasselbe T wie die erste Form. Im dritten Kästchen befindet sich wieder ein T. Allerdings ist es kleiner und aus diesem Grund ähnlich und nicht deckungsgleich. Die vierte und letzte Form ähnelt nicht einmal ansatzweise den anderen Formen. Aus diesem Grund ist die letzte Form mit Sicherheit nicht kongruent.
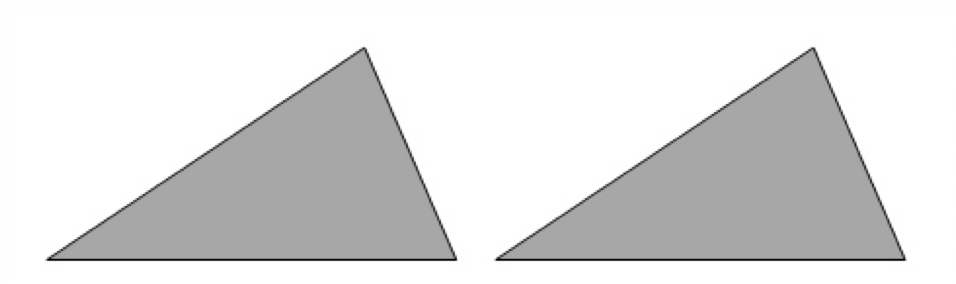
Die grauen Dreiecke sind, ohne viel zu überlegen, deckungsgleich. Durch eine Parallelverschiebung verschwindet ein Dreieck vollständig im anderen. Sie stimmen in Winkel, Seitenlänge und Größe überein.
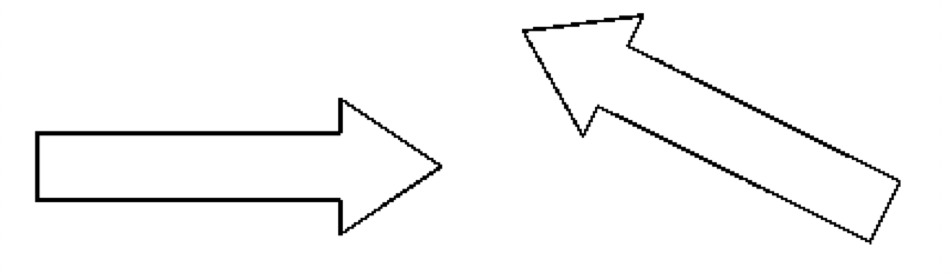
Bei den Pfeilen ist es nicht auf den ersten Blick zu erkennen. Bei diesem Beispiel ist es notwendig, die Pfeile gleich auszurichten. Entweder dreht der Anwender den rechten Pfeil bis beide nach rechts zeigen, oder er spiegelt die Formen an der Pfeilspitze. Nach einer Kongruenzbildung ist zu erkennen, dass diese Formen kongruent sind.
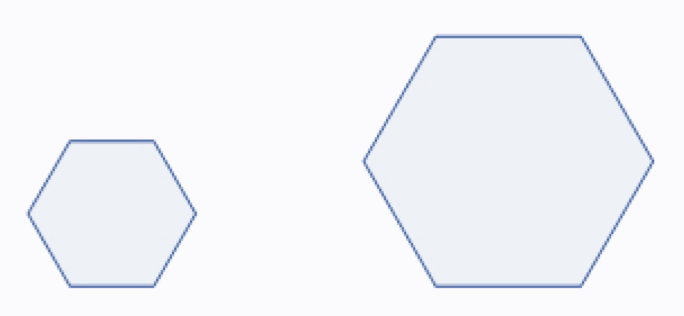
Diese Sechsecke besitzen dieselben Winkel, die gleiche Ausrichtung und sind parallel zu einander. Was auffällt, ist, dass die linke Form kleiner als die rechte ist. Kommt es zu einer Kongruenzbildung, zu einer Verschiebung einer Form, ist es nicht möglich, beide vollständig einander abzudecken. Aus diesem Grund sind diese Formen nicht kongruent, sondern gelten als ähnlich.
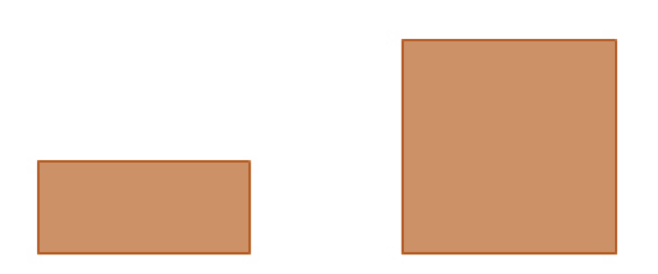
Bei diesen Vierecken stimmen die Winkel, die Ausrichtung und zwei Seitenlängen. Die jeweilige Breite dieser Formen entspricht der gleichen. Was sofort ins Auge fällt, ist, dass die Höhe unterschiedlich ist. Das linke Viereck ist halb so hoch wie das rechte. Klappt der Mathematiker die Formen aufeinander, ist zu erkennen, dass die Hälfte des höheren Vierecks alleine bleibt. Da weder die Form, noch die Größe übereinstimmen, sind diese Figuren nicht kongruent.
Kongruente Dreiecke – Beispiele
Stehen sich zwei Dreiecke gegenüber, ist es nicht immer leicht, sofort zu erkennen, ob diese deckungsgleich sind. Für diesen Zweck finden sich anschließend zwei Dreiecke, bei denen sich die Frage nach der Kongruenz stellt.
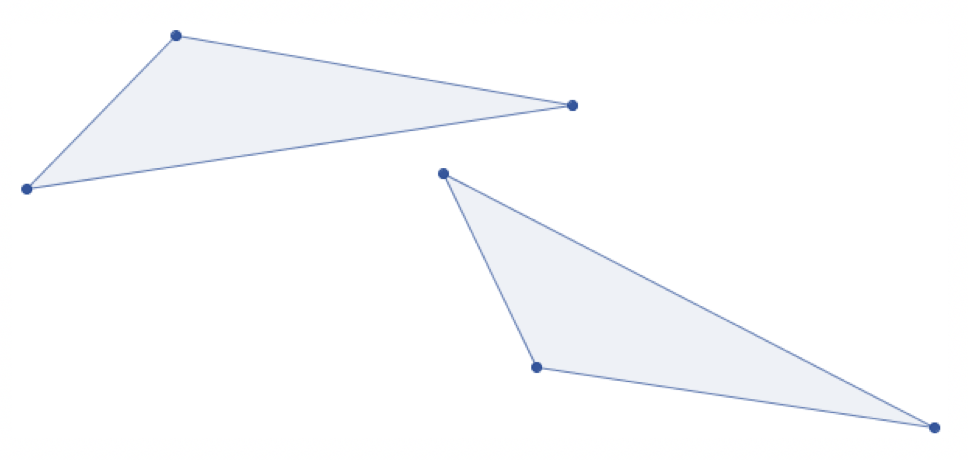
Auf den ersten Blick sind es zwei schiefwinklige Dreiecke, die nicht in die gleiche Richtung ausgerichtet sind. Eine Möglichkeit, die Ausrichtung zusammenzuführen, ist, die Dreiecke an einer Achse oder an einem Punkt zu spiegeln. Für diesen Zweck zeichnet der Anwender eine räumliche Achse und stellt beide Dreiecke gegenüber. Der Mathematiker sucht sich ein Eck aus und setzt es direkt neben der Spiegelachse. Es bietet sich an, einen Punkt an der Hypotenuse zu nehmen, da auf diese Weise die Lösung leichter zu erkennen ist.
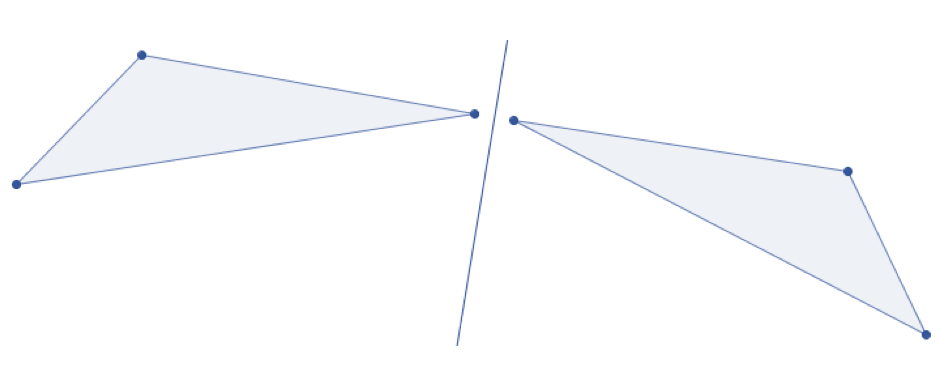
Die Achsenspiegelung macht deutlich, dass es sich bei den vorgegebenen Dreiecken, um kongruente Formen handelt. An dieser Stelle ist es möglich, das eine Dreieck über das andere zu klappen, was die Kongruenz ausmacht.
Eine zweite Möglichkeit, um die Deckungsgleichheit herauszufinden, ist eine Punktspiegelung. Der Mathematiker zeichnet einen Punkt. Rechts und links daneben, zeichnet er im gleichen Abstand die Dreiecke ein. Am besten gelingt die Spiegelung, indem ein bestimmter Eckpunkt in derselben Achse liegen, wie der Spiegelungspunkt. Sind beide Dreiecke die jeweiligen Spiegelbilder des anderen, bedeutet es, dass die Formen kongruent sind.
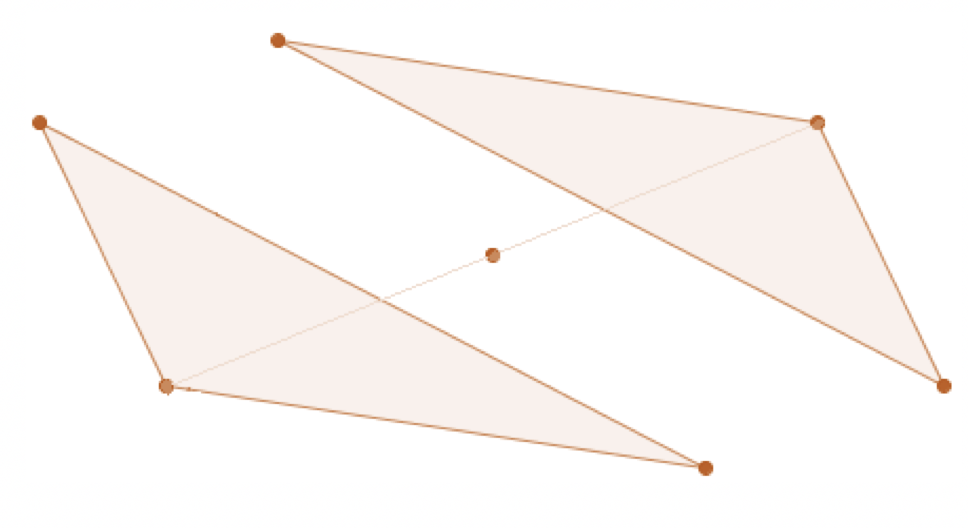
Kongruenz bei Dreiecken
Ob Dreiecke kongruent sind, erkennt der Anwender mit der Hilfe von fünf Kongruenzsätzen. Diese Sätze behandelt das nächste Thema ausführlich und verständlich. An dieser Stelle folgt eine kurze Übersicht über die Merksätze.
Sie liefern einfache Anhaltspunkte, um zu erkennen, ob die geometrischen Formen deckungsgleich sind. Kongruente Dreiecke stimmen in diesem Sinne immer entweder in
- drei Seitenlängen SSS,
- zwei Seitenlängen und derselbe eingeschlossene Winkel SWS,
- zwei Seitenlängen und derselbe gegenüberliegende Winkel SSW,
- einer Seitenlänge und dieselben anliegenden Winkel WSW oder
- einer Seitenlänge und derselbe anliegende und gegenüberliegende Winkel WWS
überein. Kommt einer dieser Merksätze zum Einsatz, stimmen alle anderen Seitenlängen sowie Winkel überein. Die Folge ist, dass die Dreiecke kongruent sind.
Kongruent – Tipps zum Lernen
Viele Schüler machen bei Klassenarbeiten dieselben Fehler. Aus diesem Grund folgen einige Tipps, was es bei kongruenten Dreiecken zu beachten gilt. Oft verwechseln Schüler, dass „kongruent“ „flächengleich“ anstelle von „deckungsgleich“ bedeutet. „Flächengleich“ heißt allerdings, dass die Fläche der beiden Formen gleich ist. Diese Figuren sind nicht zwingend kongruent, weil sie meist nicht die gleiche Form besitzen.
Eine Skizze zu machen, ist die halbe Rechnung. Eine kleine Skizze hilft beim Denken, sodass die Lösung viel leichter fällt. Es ist wichtig, alle Kongruenzsätze zu beherrschen. Selbst die Reihenfolge ist bei bestimmten Sätzen wichtig einzuhalten. Die Seiten- und Winkelangaben sollten im besten Fall der Reihenfolge eines Kongruenzsatzes entsprechen. Nicht immer reicht die Angabe aus, um zu ermitteln, ob es sich bei den angegebenen Formen um kongruente Figuren handelt.
Mit diesen Tipps und der Erklärung, was kongruent bedeutet, steht dem Einstieg ins nächste Thema nichts im Wege. Im nächsten Kapitel lernt der Leser die verschiedenen Kongruenzsätze kennen und wie diese anzuwenden sind.
