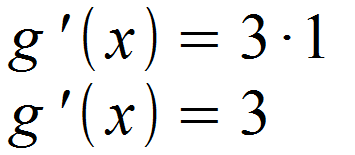Gefällt Dir unsere Seite?

Gib einfach eine Bewertung ab.

4.0 / 5

Befindet sich ein Faktor vor der Potenz, der unabhängig von der Variablen x ist, wird dieser in der Ableitung übernommen.

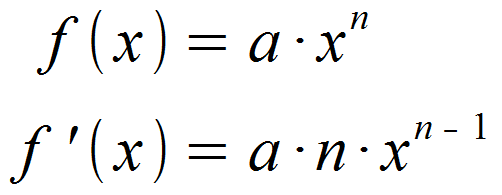
Es wird also regulär nach der Potenzregel abgeleitet und die Faktoren a und n multipliziert.
 

Beispiel 1

• Die Klammern wurden hier nur zur Veranschaulichung verwendet und haben mathematisch keine Notwendigkeit.

Folgende Funktion soll nach der Faktorregel abgeleitet werden.

Wir identifizieren n = 5 sowie a = 2 und setzen dies in die Formel ein.

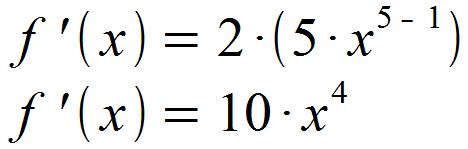
Als Ergebnis erhalten wir a · n = 10 für den Faktor vor der Potenz und 5 - 1 = 4 für den Exponenten.

Beispiel 2

Für die folgende lineare Funktion ist das zweite Beispiel aus dem Kapitel Potenzregel zu beachten.

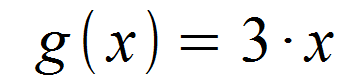
Da die Ableitung von f (x) = x gleich f '(x) = 1 ist, bleibt lediglich der Faktor a = 3 übrig.